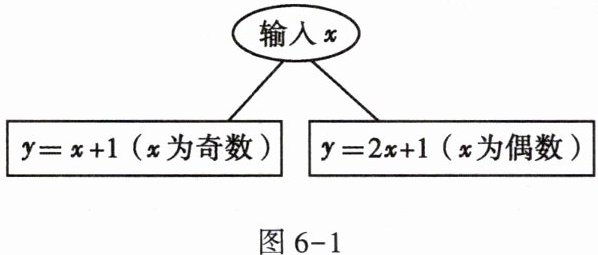
1. 小亮设计了一个数值转换程序(如图6 - 1)。当小亮输入$x = 6$时,$y$的值为()
A. 6
B. 7
C. 12
D. 13

A. 6
B. 7
C. 12
D. 13
答案:
D
2. 某轿车行驶时油箱中余油量$Q$与行驶时间$t$的关系如下表,用时间$t$表示余油量$Q$的关系式是()
|行驶时间$t/h$|余油量$Q/L$|
|----|----|
|1|$40 - 6$|
|2|$40 - 12$|
|3|$40 - 18$|
|4|$40 - 24$|
|5|$40 - 30$|
|…|…|
A. $Q = 40 - 3t$
B. $Q = 40 - t$
C. $t = 40 - 6Q$
D. $Q = 40 - 6t$
|行驶时间$t/h$|余油量$Q/L$|
|----|----|
|1|$40 - 6$|
|2|$40 - 12$|
|3|$40 - 18$|
|4|$40 - 24$|
|5|$40 - 30$|
|…|…|
A. $Q = 40 - 3t$
B. $Q = 40 - t$
C. $t = 40 - 6Q$
D. $Q = 40 - 6t$
答案:
D
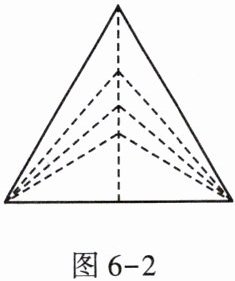
3. 如图6 - 2,三角形底边长为8cm,当它的高由小到大变化时,三角形的面积也随之发生变化。
(1)在这个变化过程中,高是____,三角形的面积是____;
(2)若三角形的高为$h$cm,则它的面积$S$ $cm^2$表示为____;
(3)当高由1cm变化到5cm时,面积从____ $cm^2$变化到____ $cm^2$;
(4)当高为3cm时,面积为____ $cm^2$;
(5)当高为10cm时,面积为____ $cm^2$。
(1)在这个变化过程中,高是____,三角形的面积是____;
(2)若三角形的高为$h$cm,则它的面积$S$ $cm^2$表示为____;
(3)当高由1cm变化到5cm时,面积从____ $cm^2$变化到____ $cm^2$;
(4)当高为3cm时,面积为____ $cm^2$;
(5)当高为10cm时,面积为____ $cm^2$。

答案:
【解析】:
(1)在这个变化过程中,因为高的变化引起了面积的变化,所以高是自变量,三角形的面积是因变量。
(2)根据三角形面积公式$S = \frac{1}{2}\times底\times高$,已知底边长为$8cm$,高为$h cm$,则它的面积$S=\frac{1}{2}\times8\times h = 4h$ $cm^2$。
(3)当$h = 1cm$时,$S = 4\times1 = 4$ $cm^2$;当$h = 5cm$时,$S = 4\times5 = 20$ $cm^2$,所以面积从$4$ $cm^2$变化到$20$ $cm^2$。
(4)当$h = 3cm$时,$S = 4\times3 = 12$ $cm^2$。
(5)当$h = 10cm$时,$S = 4\times10 = 40$ $cm^2$。
【答案】:
(1)自变量,因变量;
(2)$S = 4h$;
(3)$4$,$20$;
(4)$12$;
(5)$40$。
(1)在这个变化过程中,因为高的变化引起了面积的变化,所以高是自变量,三角形的面积是因变量。
(2)根据三角形面积公式$S = \frac{1}{2}\times底\times高$,已知底边长为$8cm$,高为$h cm$,则它的面积$S=\frac{1}{2}\times8\times h = 4h$ $cm^2$。
(3)当$h = 1cm$时,$S = 4\times1 = 4$ $cm^2$;当$h = 5cm$时,$S = 4\times5 = 20$ $cm^2$,所以面积从$4$ $cm^2$变化到$20$ $cm^2$。
(4)当$h = 3cm$时,$S = 4\times3 = 12$ $cm^2$。
(5)当$h = 10cm$时,$S = 4\times10 = 40$ $cm^2$。
【答案】:
(1)自变量,因变量;
(2)$S = 4h$;
(3)$4$,$20$;
(4)$12$;
(5)$40$。
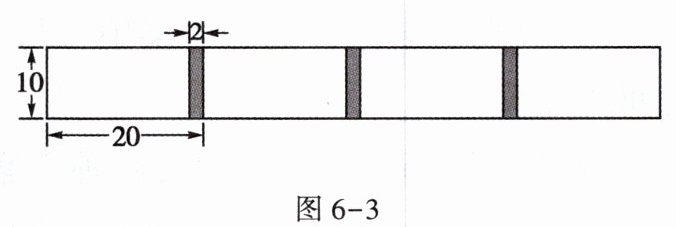
4. 将若干张长为20cm、宽为10cm的长方形白纸按图6 - 3所示的方法黏合起来,黏合部分的宽为2cm。
(1)求4张白纸黏合后的总长度;
(2)设$x$张白纸黏合后的总长度为$y$cm,写出$y$与$x$之间的关系式,并求当$x = 20$时$y$的值。
(1)求4张白纸黏合后的总长度;
(2)设$x$张白纸黏合后的总长度为$y$cm,写出$y$与$x$之间的关系式,并求当$x = 20$时$y$的值。

答案:
【解析】:
(1)$4$张白纸黏合,有$3$个黏合部分。
每张纸长$20cm$,$4$张纸不黏合时总长度为$20\times4 = 80cm$,黏合部分共$2\times3 = 6cm$。
所以$4$张白纸黏合后的总长度为$80 - 6=74cm$。
(2)$x$张白纸黏合,有$(x - 1)$个黏合部分。
每张纸长$20cm$,则$y = 20x-2(x - 1)$,化简可得$y = 18x + 2$。
当$x = 20$时,$y=18\times20 + 2=360 + 2 = 362cm$。
【答案】:
(1)$74cm$;
(2)$y = 18x + 2$,$362cm$。
(1)$4$张白纸黏合,有$3$个黏合部分。
每张纸长$20cm$,$4$张纸不黏合时总长度为$20\times4 = 80cm$,黏合部分共$2\times3 = 6cm$。
所以$4$张白纸黏合后的总长度为$80 - 6=74cm$。
(2)$x$张白纸黏合,有$(x - 1)$个黏合部分。
每张纸长$20cm$,则$y = 20x-2(x - 1)$,化简可得$y = 18x + 2$。
当$x = 20$时,$y=18\times20 + 2=360 + 2 = 362cm$。
【答案】:
(1)$74cm$;
(2)$y = 18x + 2$,$362cm$。
查看更多完整答案,请扫码查看


