《2025年暑假作业本大象出版社七年级数学北师大版》

1. 下列各式能用平方差公式计算的是()
A. $(x + 2y)(2x - y)$
B. $(x + y)(x - 2y)$
C. $(x + 2y)(2y - x)$
D. $(x - 2y)(2y - x)$

答案： 【解析】：平方差公式为$(a + b)(a - b)=a^{2}-b^{2}$，即两个二项式相乘，一项完全相同，另一项互为相反数。选项A中两项都不满足平方差公式的特征；选项B中两项也不满足平方差公式的特征；选项C中$(x + 2y)(2y - x)=(2y + x)(2y - x)$，$2y$这一项相同，$x$与$-x$互为相反数，能用平方差公式计算；选项D中$(x - 2y)(2y - x)=-(x - 2y)(x - 2y)=-(x - 2y)^{2}$，不满足平方差公式的特征。
【答案】：C

2. 计算：$2025^{2}-2026×2024=$____。

答案： 【解析】：本题可先将$2026\times2024$进行变形，再利用平方差公式进行简便计算。
- **步骤一：对$2026\times2024$进行变形**
将$2026$变形为$(2025 + 1)$，将$2024$变形为$(2025 - 1)$，则$2026\times2024=(2025 + 1)\times(2025 - 1)$。
- **步骤二：利用平方差公式计算$(2025 + 1)\times(2025 - 1)$**
平方差公式为$(a+b)(a-b)=a^2-b^2$，在$(2025 + 1)\times(2025 - 1)$中，$a = 2025$，$b = 1$，则$(2025 + 1)\times(2025 - 1)=2025^2 - 1^2=2025^2 - 1$。
- **步骤三：计算$2025^2 - 2026\times2024$**
将$2026\times2024=2025^2 - 1$代入$2025^2 - 2026\times2024$可得：
$2025^2 - (2025^2 - 1)=2025^2 - 2025^2 + 1 = 1$
【答案】：$1$

3. 化简：$(-a + b)(-a - b)=$____。

答案： 【解析】：本题可利用平方差公式$(m + n)(m - n)=m^2 - n^2$来化简$(-a + b)(-a - b)$，在$(-a + b)(-a - b)$中，可将$-a$看作公式中的$m$，$b$看作公式中的$n$，则$(-a + b)(-a - b)=(-a)^2 - b^2=a^2 - b^2$。
【答案】：$a^2 - b^2$

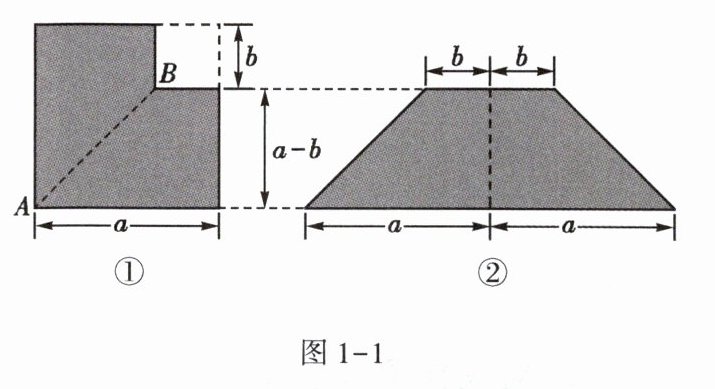
4. 如图1-1①，从边长为$a$的正方形纸片中剪去一个边长为$b$的小正方形，再沿着线段$AB$剪开，把剪成的两张纸拼成如图1-1②所示的等腰梯形。
(1) 设图1-1①中阴影部分的面积为$S_{1}$，图1-1②中阴影部分的面积为$S_{2}$，请直接用含$a,b$的代数式表示$S_{1}$和$S_{2}$；
(2) 请写出上述过程所揭示的乘法公式。

答案： 【解析】：
1. 首先求$S_1$：
图1 - 1①中阴影部分的面积是边长为$a$的正方形的面积减去边长为$b$的小正方形的面积。
根据正方形面积公式$S = 边长\times边长$，边长为$a$的正方形面积为$a^2$，边长为$b$的正方形面积为$b^2$，所以$S_1=a^{2}-b^{2}$。
2. 然后求$S_2$：
图1 - 1②是一个等腰梯形，根据梯形面积公式$S=\frac{(上底 + 下底)\times高}{2}$。
观察图形可知，该梯形的上底为$2b$，下底为$2a$，高为$(a - b)$。
则$S_2=\frac{(2b + 2a)(a - b)}{2}$，化简$\frac{(2b + 2a)(a - b)}{2}=(a + b)(a - b)$。
3. 最后得出乘法公式：
因为$S_1 = S_2$（图形只是经过剪拼，面积不变），即$a^{2}-b^{2}=(a + b)(a - b)$，这就是平方差公式。
【答案】：
(1)$S_{1}=a^{2}-b^{2}$，$S_{2}=(a + b)(a - b)$；
(2)$a^{2}-b^{2}=(a + b)(a - b)$

1. 化简$(x - 3)^{2}-x(x - 6)$的结果为()
A. $6x - 9$
B. $-12x + 9$
C. $9$
D. $3x + 9$

答案： C

2. 若$(x - 4)^{2}=x^{2}+2(m - 3)x + 16$，则$m$的值为____。

答案： $-1$

3. 若$a + b = 3,a^{2}+b^{2}=7$，则$ab$的值为____。

答案： $1$