4. 如图4-19,已知$AB = CD$,$BC = DA$,$E,F$是$AC$上的两点,且$AE = CF$,$DE = BF$,那么图中全等三角形有______对。(不添加其他辅助线)


答案:
$3$
5. 如图4-20,点$A,D,C,B$在同一条直线上,$AD = BC$,$AE = BF$,$CE = DF$,试说明$AE// BF$。


答案:
【解析】:
因为$AD = BC$,所以$AD + DC = BC + DC$,即$AC = BD$。
在$\triangle ACE$和$\triangle BDF$中,$\begin{cases}AE = BF\\CE = DF\\AC = BD\end{cases}$,根据“边边边”(SSS)定理,可得$\triangle ACE\cong\triangle BDF$。
所以$\angle A=\angle B$,根据“内错角相等,两直线平行”,可得$AE// BF$。
【答案】:
因为$AD = BC$,所以$AD + DC = BC + DC$,即$AC = BD$。
在$\triangle ACE$和$\triangle BDF$中,$\begin{cases}AE = BF\\CE = DF\\AC = BD\end{cases}$,所以$\triangle ACE\cong\triangle BDF(SSS)$。
所以$\angle A=\angle B$,所以$AE// BF$。
因为$AD = BC$,所以$AD + DC = BC + DC$,即$AC = BD$。
在$\triangle ACE$和$\triangle BDF$中,$\begin{cases}AE = BF\\CE = DF\\AC = BD\end{cases}$,根据“边边边”(SSS)定理,可得$\triangle ACE\cong\triangle BDF$。
所以$\angle A=\angle B$,根据“内错角相等,两直线平行”,可得$AE// BF$。
【答案】:
因为$AD = BC$,所以$AD + DC = BC + DC$,即$AC = BD$。
在$\triangle ACE$和$\triangle BDF$中,$\begin{cases}AE = BF\\CE = DF\\AC = BD\end{cases}$,所以$\triangle ACE\cong\triangle BDF(SSS)$。
所以$\angle A=\angle B$,所以$AE// BF$。
1. 如图4-21,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A. 带①去
B. 带②去
C. 带③去
D. 带①和②去

A. 带①去
B. 带②去
C. 带③去
D. 带①和②去
答案:
C
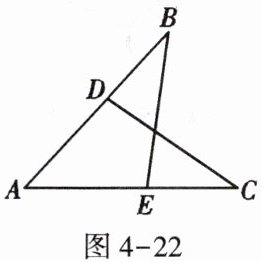
2. 如图4-22,已知点$D$在$AB$上,点$E$在$AC$上,且$∠B = ∠C$,那么补充下列一个条件后,仍无法说明$\triangle ABE≌\triangle ACD$的是( )
A. $AB = AC$
B. $∠AEB = ∠ADC$
C. $BE = CD$
D. $AD = AE$

A. $AB = AC$
B. $∠AEB = ∠ADC$
C. $BE = CD$
D. $AD = AE$
答案:
B
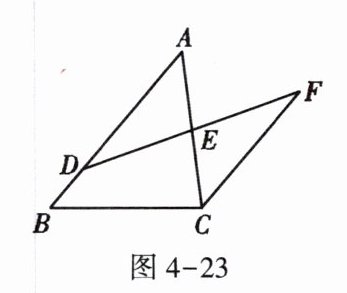
3. 如图4-23,$D$是$AB$上一点,$DF$交$AC$于点$E$,$DE = FE$,$FC// AB$。若$AB = 4$,$CF = 3$,则线段$BD$的长是________。

答案:
$1$
4. 如图4-24,在$Rt\triangle ABC$中,$∠ABC = 90^{\circ}$,点$D$在边$AB$上,使$DB = BC$,过点$D$作$EF⊥AC$,分别交$AC$于点$E$,交$CB$的延长线于点$F$。请说明$AB = BF$。


答案:
【解析】:
因为$EF\perp AC$,所以$\angle F + \angle C = 90^{\circ}$。
又因为$\angle ABC = 90^{\circ}$,所以$\angle A + \angle C = 90^{\circ}$,则$\angle A=\angle F$。
在$\triangle FBD$和$\triangle ABC$中,$\left\{\begin{array}{l}\angle FBD=\angle ABC = 90^{\circ}\\\angle F=\angle A\\DB = BC\end{array}\right.$。
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle FBD\cong\triangle ABC$。
因为全等三角形的对应边相等,所以$AB = BF$。
【答案】:$AB = BF$
因为$EF\perp AC$,所以$\angle F + \angle C = 90^{\circ}$。
又因为$\angle ABC = 90^{\circ}$,所以$\angle A + \angle C = 90^{\circ}$,则$\angle A=\angle F$。
在$\triangle FBD$和$\triangle ABC$中,$\left\{\begin{array}{l}\angle FBD=\angle ABC = 90^{\circ}\\\angle F=\angle A\\DB = BC\end{array}\right.$。
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle FBD\cong\triangle ABC$。
因为全等三角形的对应边相等,所以$AB = BF$。
【答案】:$AB = BF$
查看更多完整答案,请扫码查看


