《2025年暑假作业本大象出版社八年级数学华师大版》

5. 如图19-19，矩形ABCD中，对角线AC的垂直平分线EF分别交BC，AD于点E，F，若BE = 3，AF = 5，则AC的长为 (A)

A. $ \sqrt { 80 } $ B. $ \sqrt { 48 } $
C. 10 D. 8

答案： A

6. 如图19-20，以矩形ABCD的A点为圆心，AD长为半径画弧，交AB于F点；再以C点为圆心，CD长为半径画弧，交AB于E点. 若AD = 5，CD = $ \frac { 17 } { 3 } $，则EF的长度为 (2)
A. 2
B. 3
C. $ \frac { 2 } { 3 } $
D. $ \frac { 7 } { 3 } $

答案： A 提示：连接 CE，则 $ CE = CD = \frac{17}{3} $，$ BC = AD = 5 $。
∵ $ \triangle BCE $ 为直角三角形，
∴ $ BE = \sqrt{(\frac{17}{3})^2 - 5^2} = \frac{8}{3} $。又
∵ $ BF = AB - AF = \frac{17}{3} - 5 = \frac{2}{3} $，
∴ $ EF = BE - BF = \frac{8}{3} - \frac{2}{3} = 2 $。

1. 如图19-21，在菱形ABCD中，$ \angle B = 60 ^ { \circ } $，点E，F分别从点B，D同时以同样的速度沿边BC，DC向点C运动. 给出以下四个结论：

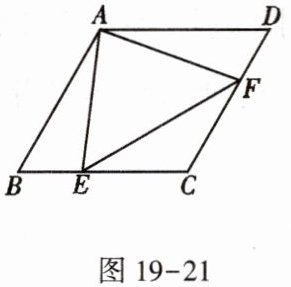
① AE = AF；
② $ \angle CEF = \angle CFE $；
③ 当点E，F分别为边BC，DC的中点时，$ \triangle AEF $是等边三角形；
④ 当点E，F分别为边BC，DC的中点时，$ \triangle AEF $的面积最大.
上述正确结论的序号有①②③.

答案： ①②③

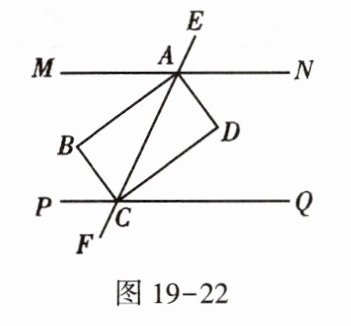
2. 如图19-22，已知MN $ // $ PQ，EF与MN，PQ分别交于A，C两点，过A，C两点作两组内错角的平分线，分别交于点B，D，则四边形ABCD是矩形.

答案： 矩形

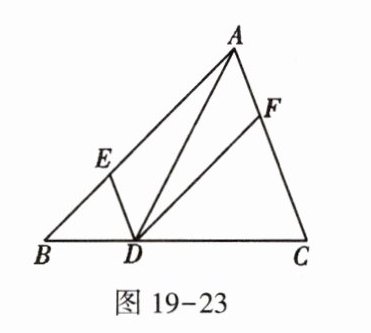
3. 如图19-23，在$ \triangle ABC $中，D是边BC上一动点，DE $ // $ AC，DF $ // $ AB，对$ \triangle ABC $及线段AD添加条件，使得四边形AEDF是正方形：$ \triangle ABC $是等腰直角三角形，AD是角平分线.

答案： $ \triangle ABC $是等腰直角三角形，AD是角平分线

4. 如图19-24，在矩形ABCD中，AB = 3，AD = 5，点E在DC上，将矩形ABCD沿AE折叠，点D恰好落在BC边上的点F处，那么$ \triangle EFC $的面积为$\frac{2}{3}$.

答案： $ \frac{2}{3} $ 提示：
∵ 四边形 ABCD 为矩形，
∴ $ AD = BC = 5 $，$ AB = CD = 3 $。
∵ 矩形 ABCD 沿 AE 折叠，顶点 D 恰好落在 BC 边上的 F 处，
∴ $ AF = AD = 5 $，$ EF = DE $。在 $ Rt \triangle ABF $ 中，
∵ $ BF = \sqrt{AF^2 - AB^2} = 4 $，
∴ $ CF = BC - BF = 5 - 4 = 1 $。设 $ CE = x $，则 $ DE = EF = 3 - x $。在 $ Rt \triangle ECF $ 中，
∵ $ CE^2 + CF^2 = EF^2 $，
∴ $ x^2 + 1^2 = (3 - x)^2 $。解得 $ x = \frac{4}{3} $，
∴ $ S_{\triangle EFC} = \frac{1}{2}CE \cdot CF = \frac{2}{3} $。