《2025年暑假作业本大象出版社八年级数学华师大版》

1. 验光师测得一组关于近视眼镜的度数$y$(单位:度)与镜片焦距$x$(单位:米)的对应数据如下表.

根据表中数据,可得$y$关于$x$的函数表达式为 (A)
A. $y=\frac{100}{x}$
B. $y=\frac{x}{100}$
C. $y=\frac{400}{x}$
D. $y=\frac{x}{400}$

答案： A

2. 若反比例函数$y=\frac{k-1}{x}$的图象位于第二、四象限,则$k$的取值可以是 (A)
A. 0
B. 1
C. 2
D. 以上都不是

答案： A

3. 对于反比例函数$y=-\frac{2}{x}$,下列说法不正确的是 (D)
A. 图象分布在第二、四象限
B. 当$x＞0$时,$y$随$x$的增大而增大
C. 图象经过点$(1,-2)$
D. 若点$A(x_1,y_1),B(x_2,y_2)$都在图象上,且$x_1＜x_2$,则$y_1＜y_2$

答案： D

4. 如图17-13,在直角坐标系$xOy$中,点$A,B,C$为反比例函数$y=\frac{k}{x}(k＞0)$上不同的三点,连接$OA,OB,OC$,过点$A$作$AD\perp y$轴于点$D$,过点$B,C$分别作$BE,CF$垂直$x$轴于点$E,F$,$OC$与$BE$相交于点$M$,记$△AOD,△BOM$,四边形$CMEF$的面积分别为$S_1,S_2,S_3$,则 (B)

A. $S_1=S_2+S_3$
B. $S_2=S_3$
C. $S_3＞S_2＞S_1$
D. $S_1S_2＜S_3^2$

答案： B

5. 如图17-14,在平面直角坐标系中,过点$M(0,2)$的直线与$x$轴平行,且直线分别与反比例函数$y=\frac{6}{x}(x＞0)$和$y=\frac{k}{x}(x＜0)$的图象交于点$P,Q$.

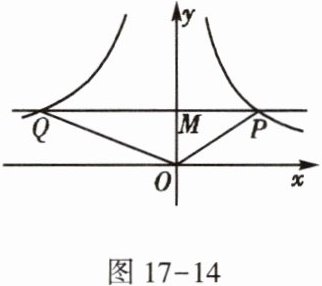
(1)求点$P$的坐标;
(2)若$△POQ$的面积为8,求$k$的值.
(1)∵　PQ//x轴,∴　点P的纵坐标为2.当y = 2时,$\frac{6}{x} = 2$,∴　x = 3,∴　点P的坐标为((3,2)). (2)∵　$S_{\triangle POQ} = \frac{1}{2}PQ \cdot OM$,∴　$\frac{1}{2}PQ \cdot 2 = 8$,∴　PQ = 8.∵　PM = 3,∴　QM = 5,∴　Q(−5,2),代入y = $\frac{k}{x}$,得k = -10.

答案：
(1)
∵　PQ//x轴,
∴　点P的纵坐标为2.当y = 2时,$\frac{6}{x} = 2$,
∴　x = 3,
∴　点P的坐标为(3,2).
(2)
∵　$S_{\triangle POQ} = \frac{1}{2}PQ \cdot OM$,
∴　$\frac{1}{2}PQ \cdot 2 = 8$,
∴　PQ = 8.
∵　PM = 3,
∴　QM = 5,
∴　Q(−5,2),代入y = $\frac{k}{x}$,得k = -10.