1. 如图17-7,在矩形$AOBC$中,$A(-2,0),B(0,1)$.若正比例函数$y=kx$的图象经过点$C$,则$k$的值为 (

A. $-\frac{1}{2}$
B. $\frac{1}{2}$
C. -2
D. 2
A
)
A. $-\frac{1}{2}$
B. $\frac{1}{2}$
C. -2
D. 2
答案:
A 提示:
∵ A(−2,0),B(0,1),
∴ OA=2,OB=1.
∵ 四边形AOBC是矩形,
∴ AC=OB=1,BC=OA=2,
∴ 点C的坐标为(−2,1).将点C(−2,1)代入y=kx,得1=−2k,解得k=−$\frac{1}{2}$.
∵ A(−2,0),B(0,1),
∴ OA=2,OB=1.
∵ 四边形AOBC是矩形,
∴ AC=OB=1,BC=OA=2,
∴ 点C的坐标为(−2,1).将点C(−2,1)代入y=kx,得1=−2k,解得k=−$\frac{1}{2}$.
2. 已知一次函数$y=kx+b$的图象经过点$(-1,1)$和$(1,-5)$,求当$x=5$时,函数$y$的值.
由题意,得$\begin{cases} 1 = -k + b, \\ -5 = k + b. \end{cases}$ 解得$\begin{cases} k =
由题意,得$\begin{cases} 1 = -k + b, \\ -5 = k + b. \end{cases}$ 解得$\begin{cases} k =
-3
, \\ b = -2
. \end{cases}$ 这个函数表达式为$y=-3x-2
$.当$x=5$时,$y=-17
$.
答案:
由题意,得$\begin{cases} 1 = -k + b, \\ -5 = k + b. \end{cases}$ 解得$\begin{cases} k = -3, \\ b = -2. \end{cases}$ 这个函数表达式为y=−3x−2.当x=5时,y=−3×5−2=−17.
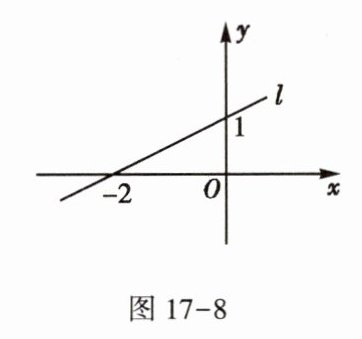
3. 如图17-8,直线$l$是一次函数$y=kx+b$的图象,若点$A(3,m)$在直线$l$上,求$m$的值.
$m=$

$m=$
$\frac{5}{2}$
答案:
由题意,得直线l过点(−2,0),(0,1),把这两点坐标代入y=kx+b,得$\begin{cases} -2k + b = 0, \\ b = 1. \end{cases}$ 解得$\begin{cases} k = \frac{1}{2}, \\ b = 1. \end{cases}$
∴ y=$\frac{1}{2}$x+1.将点A(3,m)代入,得$\frac{3}{2}$+1=m,解得m=$\frac{5}{2}$.
∴ y=$\frac{1}{2}$x+1.将点A(3,m)代入,得$\frac{3}{2}$+1=m,解得m=$\frac{5}{2}$.
查看更多完整答案,请扫码查看


