《2025年暑假作业本大象出版社八年级数学华师大版》

4. 如图17-21,$\triangle OPQ$是边长为2的等边三角形,若正比例函数的图象过点$P$,则它的表达式为$y = \sqrt{3}x$.

答案： $y = \sqrt{3}x$

1. 小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校. 如图17-22是他本次上学所用的时间$t$(单位:分)与离家的距离$s$(单位:米)的关系示意图.

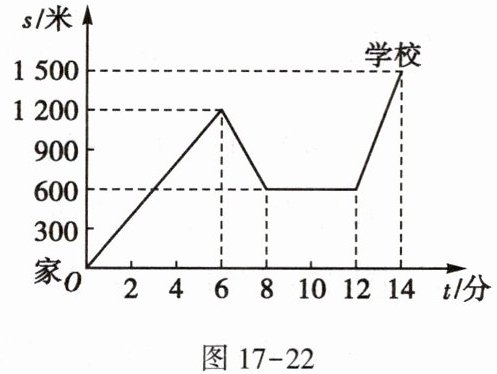
根据图中提供的信息回答下列问题:
(1)小明家到学校的距离是____1500____米.
(2)小明在书店停留了____4____分钟.
(3)本次上学途中,小明一共行驶了____2700____米,一共用了____14____分钟.
(4)我们认为骑单车的速度超过300米/分就超过了安全限度. 问:在整个上学途中哪个时间段小明的骑车速度最快? 速度在安全限度内吗?
在整个上学途中12～14分钟时间段小明的骑车速度最快, 速度不在安全限度内.

答案：
(1) $ 1500 $
(2) $ 4 $
(3) $ 2700 $ $ 14 $
(4) 当时间在 $ 0 \sim 6 $ 分钟内时, 速度为 $ 1200 \div 6 = 200 $ (米/分); 当时间在 $ 6 \sim 8 $ 分钟内时, 速度为 $ (1200 - 600) \div (8 - 6) = 300 $ (米/分); 当时间在 $ 12 \sim 14 $ 分钟内时, 速度为 $ (1500 - 600) \div (14 - 12) = 450 $ (米/分). $ \because 450 ＞ 300 $, $ \therefore $ 在整个上学途中 $ 12 \sim 14 $ 分钟时间段小明的骑车速度最快, 速度不在安全限度内.