《2025年暑假作业本大象出版社八年级数学华师大版》

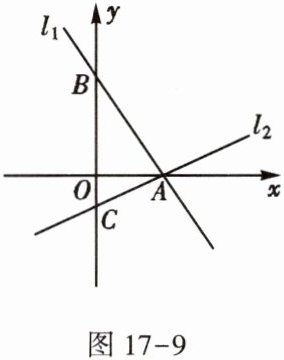
4. 如图17-9,过点$A(2,0)$的两条直线$l_1,l_2$分别交$y$轴于点$B,C$,其中点$B$在原点上方,点$C$在原点下方,$AB=\sqrt{13}$.
(1)求点$B$的坐标;(0,3)
(2)若$△ABC$的面积为4,求直线$l_2$的函数表达式.y=$\frac{1}{2}$x - 1

答案：
(1)
∵　点A(2,0),AB=$\sqrt{13}$,
∴　BO=$\sqrt{AB^2 - AO^2} = \sqrt{9} = 3$,
∴　点B的坐标为(0,3).
(2)
∵　△ABC的面积为4,
∴　$\frac{1}{2}$·BC·AO = 4,
∴　$\frac{1}{2}$·BC·2 = 4,即BC = 4.
∵　BO = 3,
∴　CO = 4 - 3 = 1,
∴　点C的坐标为(0,−1).设l₂的函数表达式为y=kx+b(k≠0),则$\begin{cases} 2k + b = 0, \\ b = -1. \end{cases}$ 解得$\begin{cases} k = \frac{1}{2}, \\ b = -1. \end{cases}$
∴　直线l₂的函数表达式为y=$\frac{1}{2}$x - 1.