《2025年暑假作业本大象出版社八年级数学华师大版》

1. 下列说法不正确的是 (D)
A. 一组邻边相等的矩形是正方形
B. 对角线相等的菱形是正方形
C. 对角线互相垂直的矩形是正方形
D. 有一个角是直角的平行四边形是正方形

答案： 1. D

2. 如图19-15,正方形ABCD的边长为1,E,F分别是对角线AC上的两点,$EG⊥AB,EI⊥AD,FH⊥AB,FJ⊥AD$,垂足分别为G,I,H,J,则图中阴影部分的面积等于 (B)
A. 1
B.$\frac {1}{2}$
C.$\frac {1}{3}$
D.$\frac {1}{4}$

答案： 2. B

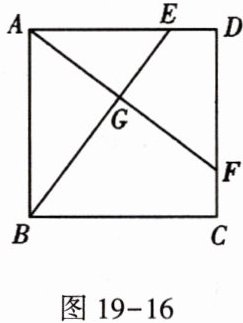
3. 如图19-16,在正方形ABCD中,点E,F分别在AD,CD上,且$DE=CF$,AF与BE相交于点G.
(1) 求证:$BE=AF$;
(2) 若$AB=4,DE=1$,求AG的长.

(1)∵ 四边形ABCD是正方形，∴ ∠BAE = ∠ADF = 90°，AB = AD = CD. ∵ DE = CF，∴ AE = DF. 在△BAE和△ADF中，
$\begin{cases}AB = AD, \\ ∠BAE = ∠ADF, \\ AE = DF,\end{cases}$
∴ △BAE ≌ △ADF(SAS)，∴ BE = AF.
(2)由(1)，得△BAE ≌ △ADF，∴ ∠EBA = ∠FAD，∴ ∠GAE + ∠AEG = 90°，∴ ∠AGE = 90°. ∵ AB = 4，DE = 1，∴ AE = 3，∴ BE = $\sqrt{AB^2 + AE^2}$ = $\sqrt{4^2 + 3^2}$ = 5. 又 ∵ 在Rt△ABE中，$\frac{1}{2}$AB × AE = $\frac{1}{2}$BE × AG，∴ AG = $\frac{AB × AE}{BE}$ = $\frac{4 × 3}{5}$ = $\frac{12}{5}$.

答案： 3.
(1)
∵ 四边形ABCD是正方形，
∴ ∠BAE = ∠ADF = 90°，AB = AD = CD.
∵ DE = CF，
∴ AE = DF. 在△BAE和△ADF中，
$\begin{cases}AB = AD, \\ ∠BAE = ∠ADF, \\ AE = DF,\end{cases}$
∴ △BAE ≌ △ADF(SAS)，
∴ BE = AF.
(2)由
(1)，得△BAE ≌ △ADF，
∴ ∠EBA = ∠FAD，
∴ ∠GAE + ∠AEG = 90°，
∴ ∠AGE = 90°.
∵ AB = 4，DE = 1，
∴ AE = 3，
∴ BE = $\sqrt{AB^2 + AE^2}$ = $\sqrt{4^2 + 3^2}$ = 5. 又
∵ 在Rt△ABE中，$\frac{1}{2}$AB × AE = $\frac{1}{2}$BE × AG，
∴ AG = $\frac{AB × AE}{BE}$ = $\frac{4 × 3}{5}$ = $\frac{12}{5}$.