《2025年暑假作业本大象出版社八年级数学华师大版》

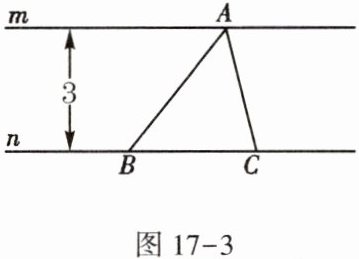
3. 如图17-3,已知直线$m,n$之间的距离是3,$△ABC$的顶点$A$在直线$m$上,边$BC$在直线$n$上,则$△ABC$的面积$S$和$BC$边的长$x$之间的关系式是S=$\frac{3}{2}$x,其中的变量是x,常量是$\frac{3}{2}$.

答案： S=$\frac{3}{2}$x　x　$\frac{3}{2}$

4. 周长为10 cm的等腰三角形,腰长$y$(单位:cm)与底边长$x$(单位:cm)的函数关系式为y=$\frac{10−x}{2}$.

答案： y=$\frac{10−x}{2}$

5. 小明从家里出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步了一段时间,然后回家.图17-4描述了小明在散步过程中离家的距离$s$(单位:米)与散步所用时间$t$(单位:分)之间的函数关系.请你由图具体说明小明散步的情况.
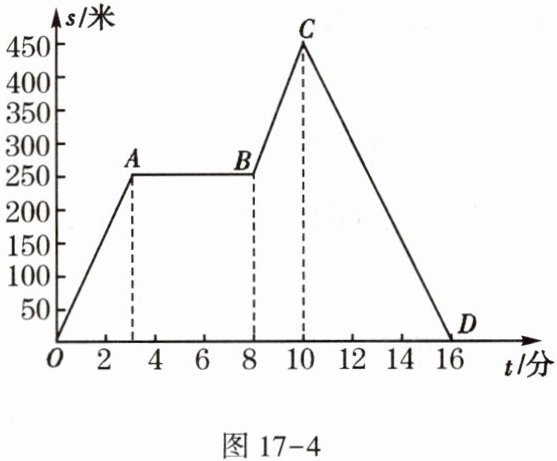
小明先走了约3分钟,到达离家250米处的一个阅报栏前看了5分钟报，又向前走了2分钟,到达离家450米处返回,走了6分钟到家.

答案： 小明先走了约3分钟,到达离家250米处的一个阅报栏前看了5分钟报，又向前走了2分钟,到达离家450米处返回,走了6分钟到家.

1. $y=\frac{\sqrt{x^2}}{x-1}$中,自变量$x$的取值范围是x≠1.

答案： x≠1

2. 函数$y=2x+4$,如果$-2\leq y\leq2$,那么$x$的取值范围是 (B)
A. $-2\leq x\leq2$
B. $-3\leq x\leq-1$
C. $1\leq x\leq3$
D. $-1\leq x\leq3$

答案： B

3. 已知$A,B$两地相距30千米,$B,C$两地相距48千米.某人骑自行车以每小时12千米的速度从$A$地出发,经过$B$地到达$C$地.设此人骑行时间为$x$(单位:时),离$B$地的距离为$y$(单位:千米).
(1)当此人在$A,B$两地之间时,求$y$与$x$的函数关系及自变量$x$的取值范围.
(2)当此人在$B,C$两地之间时,求$y$与$x$的函数关系及自变量$x$的取值范围.

答案：
(1)y=30−12x(0≤x≤2.5).　
(2)y=12x−30(2.5≤x≤6.5).