《2025年暑假作业本大象出版社八年级数学华师大版》

1. 已知关于$x$的分式方程$\frac {m-2}{x+1}=1$的解是负数，则$m$的取值范围是（$m＜3$且$m≠2$）
A. $m≤3$
B. $m≤3$且$m≠2$
C. $m＜3$
D. $m＜3$且$m≠2$

答案： D 提示：解$ \frac { m - 2 } { x + 1 } = 1 $，得$ x = m - 3 $。$ \because $关于$ x $的分式方程$ \frac { m - 2 } { x + 1 } = 1 $的解是负数，$ \therefore m - 3 ＜ 0 $，解得$ m ＜ 3 $。当$ x = m - 3 = - 1 $时，方程无解，则$ m \neq 2 $，故$ m $的取值范围是$ m ＜ 3 $且$ m \neq 2 $。

2. 要使$\frac {2x-4}{4-x}$与$\frac {x-4}{5-x}$的值互为倒数，则$x$的值为（C）
A. 0
B. 1
C. -1
D. $\frac {1}{2}$

答案： C

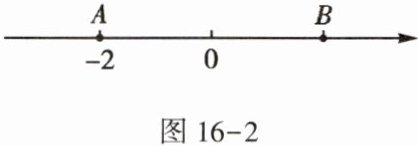
3. 如图16-2，点$A$，$B$在数轴上，它们对应的数分别为-2，$\frac {x}{x+1}$，且点$A$，$B$到原点的距离相等，则$x$的值为-2。

答案： -2

4. 已知分式方程$\frac {1}{x-2}+3=\frac {k-2}{2-x}$有增根，则$k=$1。

答案： 1

5. 已知点$P(1-2a,a-2)$在第三象限，且$a$为整数，则关于$x$的分式方程$\frac {x+1}{x-a}=2$的解是$ x = 3 $。

答案： $ x = 3 $

1. 甲、乙两班学生参加植树造林，已知甲班每天比乙班多植树5棵，甲班植80棵树所用天数与乙班植70棵树所用天数相等。若设甲班每天植树$x$棵，则根据题意列出的方程是（D）
A. $\frac {80}{x-5}=\frac {70}{x}$
B. $\frac {80}{x}=\frac {70}{x+5}$
C. $\frac {80}{x+5}=\frac {70}{x}$
D. $\frac {80}{x}=\frac {70}{x-5}$

答案： D

2. 斑马线前“车让人”，不仅体现着一座城市对生命的尊重，也直接反映着城市的文明程度。如图16-3，某路口的斑马线路段$A-B-C$横穿双向行驶车道，其中$AB=BC=6$米，在绿灯亮时，小明共用11秒通过$AC$，其中通过$BC$的速度是通过$AB$速度的1.2倍，求小明通过$AB$时的速度。设小明通过$AB$时的速度是$x$米/秒，根据题意列方程为$\frac { 6 } { x } + \frac { 6 } { 1. 2 x } = 1 1$。

答案： $ \frac { 6 } { x } + \frac { 6 } { 1. 2 x } = 1 1 $

3. 学校为创建“书香校园”购买了一批图书。已知购买科普类图书花费10000元，购买文学类图书花费9000元，其中科普类图书平均每本的价格比文学类图书平均每本的价格高25%，且购买科普类图书的数量比购买文学类图书的数量少100本。求文学类图书平均每本的价格是多少元。若设文学类图书平均每本的价格是$x$元，则可列方程为$ \frac { 9 0 0 0 } { x } - \frac { 1 0 0 0 0 } { ( 1 + 2 5 \% ) x } = 1 0 0 $。

答案： $ \frac { 9 0 0 0 } { x } - \frac { 1 0 0 0 0 } { ( 1 + 2 5 \% ) x } = 1 0 0 $