1. 菱形不具备的性质是 (
A. 四条边都相等
B. 对角线一定相等
C. 是轴对称图形
D. 是中心对称图形
B
)A. 四条边都相等
B. 对角线一定相等
C. 是轴对称图形
D. 是中心对称图形
答案:
1. B
2. 如图19-10①,在给定的一张平行四边形纸片上作一个菱形,甲、乙二人的作法如下. 甲:连接AC,作AC的垂直平分线MN,分别交AD,AC,BC于点M,O,N,连接AN,CM,则四边形ANCM是菱形,如图19-10②. 乙:作$∠BAD,∠ABC$的平分线AE,BF,分别交BC,AD于点E,F,连接EF,则四边形ABEF是菱形,如图19-10③. 根据两人的作法可判断 (


A. 甲正确,乙错误
B. 乙正确,甲错误
C. 甲、乙均正确
D. 甲、乙均错误
C
)

A. 甲正确,乙错误
B. 乙正确,甲错误
C. 甲、乙均正确
D. 甲、乙均错误
答案:
2. C
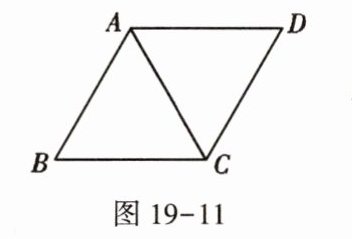
3. 如图19-11,菱形ABCD的周长是4 cm,$∠ABC=60^{\circ }$,那么这个菱形的对角线AC的长是 (
A. 1 cm
B. 2 cm
C. 3 cm
D. 4 cm
A
)
A. 1 cm
B. 2 cm
C. 3 cm
D. 4 cm
答案:
3. A
4. 如图19-12,在菱形ABCD中,对角线AC与BD相交于点O,$OE⊥AB$,垂足为E,若$∠ADC=130^{\circ }$,则$∠AOE$的度数为
65°
.
答案:
4. 65°
5. 如图19-13,若菱形ABCD的顶点A,B的坐标分别为$(3,0),(-2,0)$,点D在y轴上,则点C的坐标是____
(-5, 4)
.
答案:
5. (-5, 4)
6. 如图19-14,在平行四边形ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF. 求证:四边形AECF是菱形.
∵ 四边形ABCD是平行四边形,∴ AD = BC,AD//BC. 又 ∵ DE = BF,∴ AE = CF. ∵ AE//CF,∴ 四边形AECF是平行四边形. 又 ∵ AC⊥EF,∴ 四边形AECF是菱形.
答案:
6.
∵ 四边形ABCD是平行四边形,
∴ AD = BC,AD//BC. 又
∵ DE = BF,
∴ AE = CF.
∵ AE//CF,
∴ 四边形AECF是平行四边形. 又
∵ AC⊥EF,
∴ 四边形AECF是菱形.
∵ 四边形ABCD是平行四边形,
∴ AD = BC,AD//BC. 又
∵ DE = BF,
∴ AE = CF.
∵ AE//CF,
∴ 四边形AECF是平行四边形. 又
∵ AC⊥EF,
∴ 四边形AECF是菱形.
查看更多完整答案,请扫码查看


