1. 如图 19 - 36,在$平行四边形 ABCD$中,对角线 AC 与 BD 相交于点 O,点 E,F 分别为 OB,OD 的中点,延长 AE 至 G,使$EG = AE$,连接 CG.
(1) 求证:$△ABE\cong △CDF$.
证明:∵ 四边形 $ ABCD $ 是平行四边形,∴ $ AB = CD $,$ AB // CD $,$ OB = OD $,$ OA = OC $,∴ $ \angle ABE = \angle CDF $. ∵ 点 $ E $,$ F $ 分别为 $ OB $,$ OD $ 的中点,∴ $ BE = \frac{1}{2}OB $,$ DF = \frac{1}{2}OD $,∴ $ BE = DF $. 在 $ \triangle ABE $ 和 $ \triangle CDF $ 中,$ \begin{cases} AB = CD, \\ \angle ABE = \angle CDF, \\ BE = DF, \end{cases} $ ∴ $ \triangle ABE \cong \triangle CDF$(
(2) 当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形? 请说明理由.
当
(1) 求证:$△ABE\cong △CDF$.
证明:∵ 四边形 $ ABCD $ 是平行四边形,∴ $ AB = CD $,$ AB // CD $,$ OB = OD $,$ OA = OC $,∴ $ \angle ABE = \angle CDF $. ∵ 点 $ E $,$ F $ 分别为 $ OB $,$ OD $ 的中点,∴ $ BE = \frac{1}{2}OB $,$ DF = \frac{1}{2}OD $,∴ $ BE = DF $. 在 $ \triangle ABE $ 和 $ \triangle CDF $ 中,$ \begin{cases} AB = CD, \\ \angle ABE = \angle CDF, \\ BE = DF, \end{cases} $ ∴ $ \triangle ABE \cong \triangle CDF$(
SAS
).(2) 当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形? 请说明理由.
当
$AC = 2AB$
时,四边形 $ EGCF $ 是矩形. 理由如下:∵ $ AC = 2OA $,$ AC = 2AB $,∴ $ AB = OA $. ∵ $ E $ 是 $ OB $ 的中点,∴ $ AG \perp OB $,∴ $ \angle OEG = 90^{\circ} $. 同理:$ CF \perp OD $. ∴ $ AG // CF $,∴ $ EG // CF $. ∵ $ \triangle ABE \cong \triangle CDF $,∴ $ AE = CF $. 又∵ $ EG = AE $,∴ $ EG = CF $,∴ 四边形 $ EGCF $ 是平行四边形. ∵ $ \angle OEG = 90^{\circ} $,∴ 四边形 $ EGCF $ 是矩形.
答案:
(1)
∵ 四边形 $ ABCD $ 是平行四边形,
∴ $ AB = CD $,$ AB // CD $,$ OB = OD $,$ OA = OC $,
∴ $ \angle ABE = \angle CDF $.
∵ 点 $ E $,$ F $ 分别为 $ OB $,$ OD $ 的中点,
∴ $ BE = \frac{1}{2}OB $,$ DF = \frac{1}{2}OD $,
∴ $ BE = DF $. 在 $ \triangle ABE $ 和 $ \triangle CDF $ 中,$ \begin{cases} AB = CD, \\ \angle ABE = \angle CDF, \\ BE = DF, \end{cases} $
∴ $ \triangle ABE \cong \triangle CDF(SAS) $.
(2) 当 $ AC = 2AB $ 时,四边形 $ EGCF $ 是矩形. 理由如下:
∵ $ AC = 2OA $,$ AC = 2AB $,
∴ $ AB = OA $.
∵ $ E $ 是 $ OB $ 的中点,
∴ $ AG \perp OB $,
∴ $ \angle OEG = 90^{\circ} $. 同理:$ CF \perp OD $.
∴ $ AG // CF $,
∴ $ EG // CF $.
∵ $ \triangle ABE \cong \triangle CDF $,
∴ $ AE = CF $. 又
∵ $ EG = AE $,
∴ $ EG = CF $,
∴ 四边形 $ EGCF $ 是平行四边形.
∵ $ \angle OEG = 90^{\circ} $,
∴ 四边形 $ EGCF $ 是矩形.
(1)
∵ 四边形 $ ABCD $ 是平行四边形,
∴ $ AB = CD $,$ AB // CD $,$ OB = OD $,$ OA = OC $,
∴ $ \angle ABE = \angle CDF $.
∵ 点 $ E $,$ F $ 分别为 $ OB $,$ OD $ 的中点,
∴ $ BE = \frac{1}{2}OB $,$ DF = \frac{1}{2}OD $,
∴ $ BE = DF $. 在 $ \triangle ABE $ 和 $ \triangle CDF $ 中,$ \begin{cases} AB = CD, \\ \angle ABE = \angle CDF, \\ BE = DF, \end{cases} $
∴ $ \triangle ABE \cong \triangle CDF(SAS) $.
(2) 当 $ AC = 2AB $ 时,四边形 $ EGCF $ 是矩形. 理由如下:
∵ $ AC = 2OA $,$ AC = 2AB $,
∴ $ AB = OA $.
∵ $ E $ 是 $ OB $ 的中点,
∴ $ AG \perp OB $,
∴ $ \angle OEG = 90^{\circ} $. 同理:$ CF \perp OD $.
∴ $ AG // CF $,
∴ $ EG // CF $.
∵ $ \triangle ABE \cong \triangle CDF $,
∴ $ AE = CF $. 又
∵ $ EG = AE $,
∴ $ EG = CF $,
∴ 四边形 $ EGCF $ 是平行四边形.
∵ $ \angle OEG = 90^{\circ} $,
∴ 四边形 $ EGCF $ 是矩形.
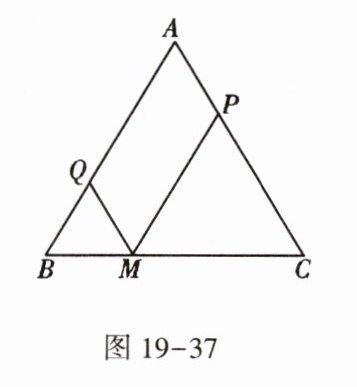
2. 如图 19 - 37,已知$△ABC$中,$AB = AC = a$,M 为底边 BC 上任意一点,过点 M 分别作 AB,AC 的平行线交 AC 于 P,交 AB 于 Q.
(1) 线段 QM,PM,AB 之间有什么关系? 说明理由.
(2) M 位于 BC 的什么位置时,四边形 AQMP 为菱形? 说明理由.
(1) 线段 QM,PM,AB 之间有什么关系? 说明理由.
(2) M 位于 BC 的什么位置时,四边形 AQMP 为菱形? 说明理由.

答案:
(1) $ QM + PM = AB $. 理由如下:
∵ $ QM // AC $,$ PM // AB $,
∴ 四边形 $ AQMP $ 是平行四边形,
∴ $ AP = QM $,$ AQ = PM $,$ \angle QMB = \angle C $.
∵ $ AB = AC $,
∴ $ \angle B = \angle C $,
∴ $ \angle B = \angle QMB $,
∴ $ BQ = QM $,
∴ $ AB = AQ + BQ = QM + PM $.
(2) 当 $ M $ 为 $ BC $ 的中点时,四边形 $ AQMP $ 是菱形. 理由如下:如图,连接 $ AM $,
∵ $ AB = AC $,$ M $ 为 $ BC $ 的中点,
∴ $ \angle BAM = \angle CAM $.
∵ $ QM // AC $,
∴ $ \angle QMA = \angle CAM $,
∴ $ \angle QAM = \angle QMA $,
∴ $ AQ = QM $.
∵ $ QM // AC $,$ PM // AB $,
∴ 四边形 $ AQMP $ 是平行四边形,
∴ 四边形 $ AQMP $ 是菱形.
(1) $ QM + PM = AB $. 理由如下:
∵ $ QM // AC $,$ PM // AB $,

∴ 四边形 $ AQMP $ 是平行四边形,
∴ $ AP = QM $,$ AQ = PM $,$ \angle QMB = \angle C $.
∵ $ AB = AC $,
∴ $ \angle B = \angle C $,
∴ $ \angle B = \angle QMB $,
∴ $ BQ = QM $,
∴ $ AB = AQ + BQ = QM + PM $.
(2) 当 $ M $ 为 $ BC $ 的中点时,四边形 $ AQMP $ 是菱形. 理由如下:如图,连接 $ AM $,
∵ $ AB = AC $,$ M $ 为 $ BC $ 的中点,
∴ $ \angle BAM = \angle CAM $.
∵ $ QM // AC $,
∴ $ \angle QMA = \angle CAM $,
∴ $ \angle QAM = \angle QMA $,
∴ $ AQ = QM $.
∵ $ QM // AC $,$ PM // AB $,
∴ 四边形 $ AQMP $ 是平行四边形,
∴ 四边形 $ AQMP $ 是菱形.
3. 如图 19 - 38,在菱形 ABCD 中,对角线 AC 与 BD 交于点 O. 过点 C 作 BD 的平行线,过点 D 作 AC 的平行线,两直线相交于点 E.
(1) 求证:四边形 OCED 是矩形;
证明:∵ 四边形 ABCD 是菱形,∴ AC⊥BD,∴ ∠COD=90°. ∵ CE//OD,DE//OC,∴ 四边形 OCED 是平行四边形. 又∵ ∠COD=90°,∴ 平行四边形 OCED 是矩形.
(2) 若CE=1,DE=2,求四边形 ABCD 的面积.
解:由(1)知,四边形 OCED 是矩形,则 CE=OD=1,DE=OC=2. ∵ 四边形 ABCD 是菱形,∴ AC=2OC=4,BD=2OD=2,∴ 菱形 ABCD 的面积为
(1) 求证:四边形 OCED 是矩形;
证明:∵ 四边形 ABCD 是菱形,∴ AC⊥BD,∴ ∠COD=90°. ∵ CE//OD,DE//OC,∴ 四边形 OCED 是平行四边形. 又∵ ∠COD=90°,∴ 平行四边形 OCED 是矩形.
(2) 若CE=1,DE=2,求四边形 ABCD 的面积.
解:由(1)知,四边形 OCED 是矩形,则 CE=OD=1,DE=OC=2. ∵ 四边形 ABCD 是菱形,∴ AC=2OC=4,BD=2OD=2,∴ 菱形 ABCD 的面积为
4
.
答案:
(1)
∵ 四边形 $ ABCD $ 是菱形,
∴ $ AC \perp BD $,
∴ $ \angle COD = 90^{\circ} $.
∵ $ CE // OD $,$ DE // OC $,
∴ 四边形 $ OCED $ 是平行四边形. 又
∵ $ \angle COD = 90^{\circ} $,
∴ 平行四边形 $ OCED $ 是矩形.
(2) 由
(1) 知,平行四边形 $ OCED $ 是矩形,则 $ CE = OD = 1 $,$ DE = OC = 2 $.
∵ 四边形 $ ABCD $ 是菱形,
∴ $ AC = 2OC = 4 $,$ BD = 2OD = 2 $,
∴ 菱形 $ ABCD $ 的面积为 $ \frac{1}{2}AC \cdot BD = \frac{1}{2} \times 4 \times 2 = 4 $.
(1)
∵ 四边形 $ ABCD $ 是菱形,
∴ $ AC \perp BD $,
∴ $ \angle COD = 90^{\circ} $.
∵ $ CE // OD $,$ DE // OC $,
∴ 四边形 $ OCED $ 是平行四边形. 又
∵ $ \angle COD = 90^{\circ} $,
∴ 平行四边形 $ OCED $ 是矩形.
(2) 由
(1) 知,平行四边形 $ OCED $ 是矩形,则 $ CE = OD = 1 $,$ DE = OC = 2 $.
∵ 四边形 $ ABCD $ 是菱形,
∴ $ AC = 2OC = 4 $,$ BD = 2OD = 2 $,
∴ 菱形 $ ABCD $ 的面积为 $ \frac{1}{2}AC \cdot BD = \frac{1}{2} \times 4 \times 2 = 4 $.
查看更多完整答案,请扫码查看


