《2025年暑假作业本大象出版社八年级数学华师大版》

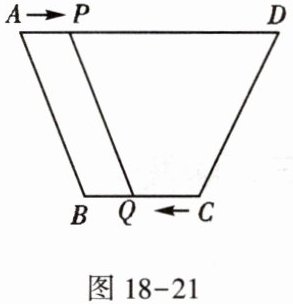
2. 如图 18-21,在四边形 ABCD 中,$ AD // BC $,且 $ AD ＞ BC $,$ BC = 6 cm $,P,Q 分别从 A,C 点同时出发,P 以 $ 1 cm/s $ 的速度由 A 向 D 运动,Q 以 $ 2 cm/s $ 的速度由 C 向 B 运动,2秒后四边形 ABQP 是平行四边形?

答案： 设经过 $x$ s 后四边形 $ABQP$ 是平行四边形，即 $AP = BQ$，由题意，得 $AP = x$，$BQ = BC - CQ = 6 - 2x$，所以 $x = 6 - 2x$，解得 $x = 2$，所以 $2$ s 后四边形 $ABQP$ 是平行四边形。

3. 如图 18-22,在□ABCD 的边 AB,CD 上截取 AF,CE,使得 $ AF = CE $,连接EF,点 M,N 是线段 EF 上两点,且 $ EM = FN $,连接 AN,CM.
(1)求证:$ △AFN \cong △CEM $;
证明：∵ 四边形 $ABCD$ 是平行四边形，∴ $CD// AB$，∴ $\angle AFN = \angle CEM$。又 ∵ $FN = EM$，$AF = CE$，∴ $\triangle AFN\cong\triangle CEM$(SAS)。
(2)若 $ ∠CMF = 107° $,$ ∠CEM = 72° $,求 $ ∠NAF $ 的度数.
解：∵ $\triangle AFN\cong\triangle CEM$，∴ $\angle NAF = \angle ECM$。∵ $\angle CMF = \angle CEM + \angle ECM$，∴ $107^{\circ}=72^{\circ}+\angle ECM$，∴ $\angle ECM = $35°，∴ $\angle NAF = $35°。

答案：
(1)
∵ 四边形 $ABCD$ 是平行四边形，
∴ $CD// AB$，
∴ $\angle AFN = \angle CEM$。又
∵ $FN = EM$，$AF = CE$，
∴ $\triangle AFN\cong\triangle CEM(SAS)$。
(2)
∵ $\triangle AFN\cong\triangle CEM$，
∴ $\angle NAF = \angle ECM$。
∵ $\angle CMF = \angle CEM + \angle ECM$，
∴ $107^{\circ}=72^{\circ}+\angle ECM$，
∴ $\angle ECM = 35^{\circ}$，
∴ $\angle NAF = 35^{\circ}$。