《2025年暑假作业本大象出版社八年级数学华师大版》

3. 如图19-27，以$ \triangle ABC $的三边为边在BC的同侧分别作三个等边三角形：$ \triangle ABD $，$ \triangle BCE $，$ \triangle ACF $，请解答下列问题：
(1) 求证：四边形AFED是平行四边形.
(2) 当$ \triangle ABC $满足什么条件时，四边形AFED是矩形？
答：当$ \triangle ABC $满足$ \angle BAC = 150^\circ $时，四边形AFED是矩形.
(3) 当$ \triangle ABC $满足什么条件时，四边形AFED是菱形？
答：当$ \triangle ABC $满足$ \angle BAC \neq 60^\circ $且$ AB = AC $时，四边形AFED是菱形.

答案：
(1)
∵ $ \triangle ABD $，$ \triangle BEC $ 都是等边三角形，
∴ $ BD = AB $，$ BE = BC $，$ \angle DBA = \angle EBC = 60^\circ $，
∴ $ \angle DBE = 60^\circ - \angle EBA $，$ \angle ABC = 60^\circ - \angle EBA $，
∴ $ \angle DBE = \angle ABC $，
∴ $ \triangle DBE \cong \triangle ABC (SAS) $，
∴ $ DE = AC $。又
∵ $ \triangle ACF $ 是等边三角形，
∴ $ AC = AF $，
∴ $ DE = AF $。同理可得 $ \triangle ABC \cong \triangle FEC $，即 $ EF = AB = DA $。
∵ $ DE = AF $，$ DA = EF $，
∴ 四边形 AFED 为平行四边形。
(2) 若四边形 AFED 为矩形，则 $ \angle DAF = 90^\circ $。
∵ $ \angle DAB = \angle FAC = 60^\circ $，
∴ $ \angle BAC = 360^\circ - \angle DAB - \angle FAC - \angle DAF = 360^\circ - 60^\circ - 60^\circ - 90^\circ = 150^\circ $，
∴ 当 $ \triangle ABC $ 满足 $ \angle BAC = 150^\circ $ 时，四边形 AFED 是矩形。
(3) 当 $ \triangle ABC $ 满足 $ \angle BAC \neq 60^\circ $ 且 $ AB = AC $ 时，四边形 AFED 是菱形。理由如下：
∵ 此时 $ AB = AC = AF = AD $，四边形 AFED 是平行四边形，
∴ 四边形 AFED 是菱形。

1. 下列说法正确的是 (D)
A. 对角线相等且互相垂直的四边形是菱形
B. 对角线相等的四边形是矩形
C. 若$a^{2}=b^{2}$,则$a=b$
D. 正方形的对角线互相平分且相等

答案： D

2. 如图 19 - 28,将$△ABC$沿 BC 方向平移得到$△DCE$,连接 AD,下列条件能够判定四边形 ABCD 为菱形的是 (A)

A. $AB = BC$
B. $AC = BC$
C. $∠B = 60^{\circ}$
D. $∠ACB = 60^{\circ}$

答案： A

3. 如图 19 - 29,在$平行四边形 ABCD$中,对角线 AC,BD 相交于点 O,$OA = 2$,若$平行四边形 ABCD$为矩形,则 OB 的长为 (C)

A. 4
B. 3
C. 2
D. 1

答案： C

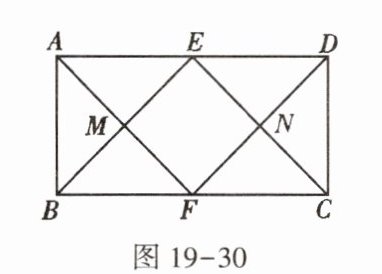
4. 如图 19 - 30,在矩形 ABCD 中,E,F 分别是 AD,BC 的中点,连接 AF,BE,CE,DF 分别交于点 M,N,四边形 EMFN 是 (B)

A. 正方形
B. 菱形
C. 矩形
D. 无法确定

答案： B