《2025年暑假作业本大象出版社八年级数学华师大版》

1. 平行四边形的两条对角线分别为6和10，则其中一条边x的取值范围为（B）
A. $4 ＜ x ＜ 6$
B. $2 ＜ x ＜ 8$
C. $0 ＜ x ＜ 10$
D. $0 ＜ x ＜ 6$

答案： B

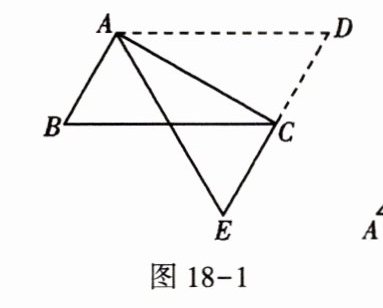
2. 如图18-1，在$□ ABCD$中，将$\triangle ADC$沿AC折叠后，点D恰好落在DC的延长线上的点E处. 若$\angle B = 60^{\circ}$，$AB = 3$，则$\triangle ADE$的周长为（C）

A. 12
B. 15
C. 18
D. 21

答案： C

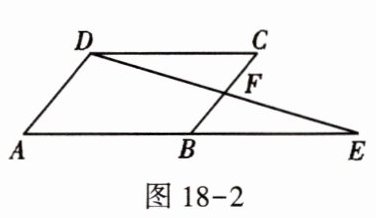
3. 如图18-2，在$□ ABCD$中，延长AB至E点，使$BE = AB$，连接DE交BC于F点，则下列结论不一定成立的是（D）

A. $\angle E = \angle CDF$
B. $EF = DF$
C. $AD = 2BF$
D. $BE = 2CF$

答案： D

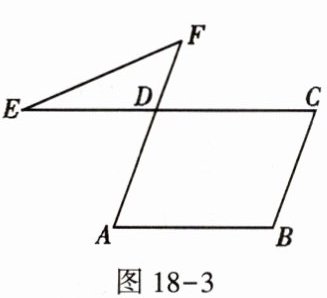
4. 如图18-3，在$□ ABCD$中，$\angle B = 110^{\circ}$，延长AD至F点，延长CD至E点，连接EF，则$\angle E + \angle F$等于（D）

A. $110^{\circ}$
B. $30^{\circ}$
C. $50^{\circ}$
D. $70^{\circ}$

答案： D

5. 如图18-4，在$□ ABCD$中，$AB = 2$，$BC = 3$. 以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于$\frac{1}{2}PQ$的长为半径画弧，两弧相交于点N，射线CN交BA的延长线于点E，则AE的长是（B）

A. $\frac{1}{2}$
B. 1
C. $\frac{6}{5}$
D. $\frac{3}{2}$

答案： B 提示:由题意,可知 CE 是$∠BCD$的平分线,$\therefore ∠BCE=∠DCE$.$\because$ 四边形 ABCD 是平行四边形,$\therefore AB// CD$,$\therefore ∠DCE=∠E$,$\therefore ∠BCE=∠AEC$,$\therefore BE=BC=3$.$\because AB=2$,$\therefore AE=BE-AB=1$.

6. 如图18-5，在$□ ABCD$中，对角线AC，BD相交于点O，过点O的一条直线分别交AD，BC于点E，F. 求证：$AE = CF$.
证明：$\because 平行四边形ABCD$的对角线 AC, BD 交于点 O,$\therefore AO=CO$,$AD// BC$,$\therefore ∠EAO=∠FCO$. 在$\triangle AOE$和$\triangle COF$中,$\left\{\begin{array}{l} ∠EAO=∠FCO,\\ AO=CO,\\ ∠AOE=∠COF,\end{array}\right. $$\therefore \triangle AOE\cong \triangle COF(ASA)$,$\therefore AE=CF$.

答案： $\because 平行四边形ABCD$的对角线 AC, BD 交于点 O,$\therefore AO=CO$,$AD// BC$,$\therefore ∠EAO=∠FCO$. 在$\triangle AOE$和$\triangle COF$中,$\left\{\begin{array}{l} ∠EAO=∠FCO,\\ AO=CO,\\ ∠AOE=∠COF,\end{array}\right. $$\therefore \triangle AOE\cong \triangle COF(ASA)$,$\therefore AE=CF$.