第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
四、巧设一般三角形为特殊的三角形
例 4 已知:如图④,在$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,点$D$,$E在AC$上,$AB = AD$,$CE = BC$,则$\angle DBE$的大小是 ()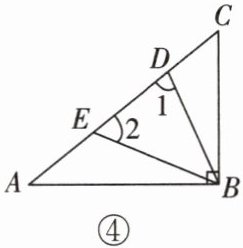
A.$60^{\circ}$
B.$45^{\circ}$
C.$30^{\circ}$
D.无法确定
例 4 已知:如图④,在$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,点$D$,$E在AC$上,$AB = AD$,$CE = BC$,则$\angle DBE$的大小是 ()

A.$60^{\circ}$
B.$45^{\circ}$
C.$30^{\circ}$
D.无法确定
答案:
例4 B
例 5 已知:如图⑤,在$\triangle ABC$中,$AB = AC$,$\angle BAD = \alpha$,且$AE = AD$,则$\angle EDC$等于 ()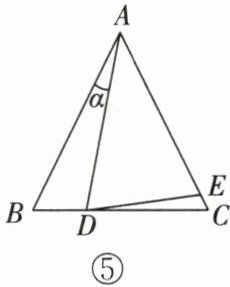
A.$\frac{1}{2}\alpha$
B.$\frac{1}{3}\alpha$
C.$\frac{1}{4}\alpha$
D.$\frac{2}{3}\alpha$

A.$\frac{1}{2}\alpha$
B.$\frac{1}{3}\alpha$
C.$\frac{1}{4}\alpha$
D.$\frac{2}{3}\alpha$
答案:
例5 A
1. 已知$a < 0$,$b > 0$,在$a + b$,$a - b$,$-a + b$,$-a - b$中,哪个式子的值最大?
答案:
解:已知a<0,b>0,可以假设a=−1,b=1,那么a+b=0,a−b=−2,−a + b=2,−a−b=0,通过计算,发现−a + b最大。
2. 已知$abc = 1$,求$\frac{a}{ab + a + 1} + \frac{b}{bc + b + 1} + \frac{c}{ac + c + 1}$的值。
答案:
解:令a=1,b=1,c=1,则
$\begin{aligned}&\frac{a}{ab + a + 1} + \frac{b}{bc + b + 1} + \frac{c}{ac + c + 1}\\=&\frac{1}{1 × 1 + 1 + 1} + \frac{1}{1 × 1 + 1 + 1} + \frac{1}{1 × 1 + 1 + 1}\\=&\frac{1}{3} + \frac{1}{3} + \frac{1}{3}\\=&1\end{aligned}$
$\begin{aligned}&\frac{a}{ab + a + 1} + \frac{b}{bc + b + 1} + \frac{c}{ac + c + 1}\\=&\frac{1}{1 × 1 + 1 + 1} + \frac{1}{1 × 1 + 1 + 1} + \frac{1}{1 × 1 + 1 + 1}\\=&\frac{1}{3} + \frac{1}{3} + \frac{1}{3}\\=&1\end{aligned}$
3. 两人用同样大小的硬币,轮流放置于一个长方形台面上,不允许互相重叠,谁放最后一枚谁就获胜。那么是先放的人获胜,还是后放的人获胜呢?
答案:
解:问题中既然没有指明台面的大小,不妨考虑一种特殊情况,即:台面充分小,以至于只能放下一枚硬币,这样的话,先放的人显然获胜。事实上,即使台面面积很大,甲首先在台面中心放一枚硬币,然后,只要乙放一枚硬币,甲就在这枚硬币关于中心对称的位置放一枚,即结论不变,依然是先放的人获胜。
查看更多完整答案,请扫码查看


