《2025年暑假作业安徽教育出版社七年级数学北师大版》

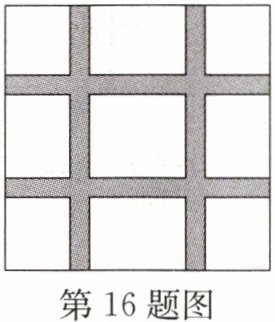
16. 如图,在一块边长为a的正方形花圃中,两纵两横的4条宽度为b的人行道把花圃分成了9块,下面是四种计算种花部分土地总面积的代数式:①$(a-2b)^{2}$;②$a^{2}-4ab$;③$a^{2}-4ab+b^{2}$;④$a^{2}-4ab+4b^{2}$。其中正确的有()


A.②
B.①③
C.①④
D.④

答案： 16. C

17. 计算$(a^{4})^{3}+a^{2}(-a^{2})^{5}+a^{6}(-a^{6})$的值。

答案： 17. 解：先运用幂的运算性质进行运算，再合并同类项。
原式 $ = a ^ { 12 } + a ^ { 2 } \cdot ( - a ^ { 10 } ) + a ^ { 6 } ( - a ^ { 6 } ) = a ^ { 12 } - a ^ { 12 } - a ^ { 12 } = - a ^ { 12 } $。

18. 若$2^{n}+2^{n}+2^{n}+2^{n}= 2$,求n的值。

答案： 18. 解：因为 $ 2 ^ { n } + 2 ^ { n } + 2 ^ { n } + 2 ^ { n } = 4 × 2 ^ { n } = 2 ^ { 2 } × 2 ^ { n } = 2 ^ { n + 2 } = 2 $，所以 $ n + 2 = 1 $，解得 $ n = - 1 $。

19. 地球和太阳可以近似看成球体。地球的半径约为$6×10^{3}km$,太阳的半径约是地球半径的$10^{2}$倍。试计算太阳的体积(π取3.14)。

答案： 19. 解：$ V = \frac { 4 } { 3 } \pi × ( 6 × 10 ^ { 3 } ) ^ { 3 } × ( 10 ^ { 2 } ) ^ { 3 } = \frac { 4 } { 3 } \pi × 6 ^ { 3 } × 10 ^ { 9 } × 10 ^ { 6 } \approx 9.0432 × 10 ^ { 17 } ( \mathrm { km } ^ { 3 } ) $。