《2025年暑假作业安徽教育出版社七年级数学北师大版》

12.如图,在△ABC中,∠C= ∠ABC= 2∠A,BD是AC边上的高,求∠DBC的度数。

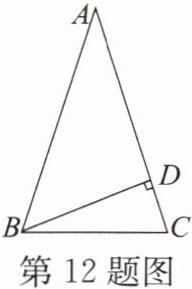
答案： 解：由题意得 $ \angle A = \frac { 180 ^ { \circ } } { 5 } = 36 ^ { \circ } $，$ \angle C = 72 ^ { \circ } $，$ \angle DBC = 90 ^ { \circ } - 72 ^ { \circ } = 18 ^ { \circ } $。

13.(2023·苏州中考)如图,在正方形网格内,线段PQ的两个端点都在格点上,网格内另有A,B,C,D四个格点。下面四个结论中,正确的是 ()

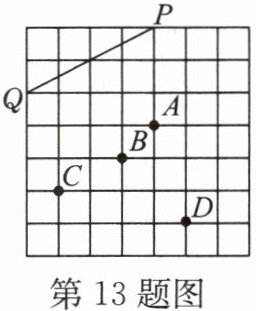
A.连接AB,则AB//PQ
B.连接BC,则BC//PQ
C.连接BD,则BD⊥PQ
D.连接AD,则AD⊥PQ

答案： B

14.将一副直角三角板按如图的方式放置,已知∠E= 60°,∠C= 45°,EF//BC,则∠BND= ____°。

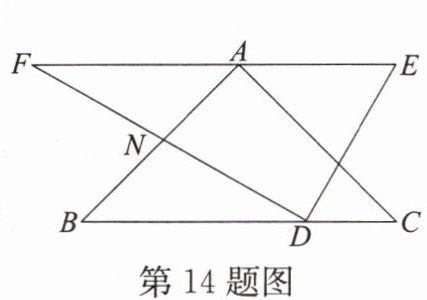
答案： 105

15.如图,已知AB= AC,BD= BC,AD= DE= EB,试求∠A的度数。

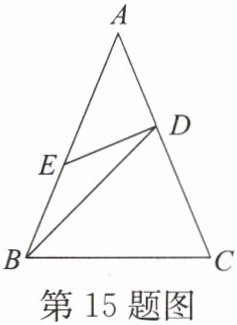
答案： 解：设 $ \angle EBD = x $。因为 $ DE = BE $，所以 $ \angle EBD = \angle BDE = x $，所以 $ \angle AED = \angle BDE + \angle DBE = 2 x $。
因为 $ AD = DE $，所以 $ \angle A = \angle AED = 2 x $，所以 $ \angle CDB = \angle A + \angle ABD = 2 x + x = 3 x $。
因为 $ BD = BC $，所以 $ \angle C = \angle BDC = 3 x $。
因为 $ AB = AC $，所以 $ \angle C = \angle ABC = 3 x $，所以 $ \angle CBD = \angle ABC - \angle ABD = 3 x - x = 2 x $。
因为 $ \angle CBD + \angle C + \angle CDB = 180 ^ { \circ } $，即 $ 2 x + 3 x + 3 x = 180 ^ { \circ } $，所以 $ x = 22.5 ^ { \circ } $，所以 $ \angle A = 2 × 22.5 ^ { \circ } = 45 ^ { \circ } $。