第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
14. (2023·临沂中考)观察下列式子:
$1×3+1= 2^{2}$;$2×4+1= 3^{2}$;$3×5+1= 4^{2}$;…。
按照上述规律,知____$=n^{2}$。
$1×3+1= 2^{2}$;$2×4+1= 3^{2}$;$3×5+1= 4^{2}$;…。
按照上述规律,知____$=n^{2}$。
答案:
$ ( n - 1 ) ( n + 1 ) + 1 $
15. 已知$|2m-1|+(n-3)^{2}= 0$,化简代数式后求值:
$[(2m+n)^{2}-(2m-n)(2m+n)-8n]÷2n$。
$[(2m+n)^{2}-(2m-n)(2m+n)-8n]÷2n$。
答案:
解: 原式 $ = ( 4 m ^ { 2 } + 4 m n + n ^ { 2 } - 4 m ^ { 2 } + n ^ { 2 } - 8 n ) ÷ 2 n = ( 4 m n + 2 n ^ { 2 } - 8 n ) ÷ 2 n = 2 m + n - 4 $。
因为 $ | 2 m - 1 | + ( n - 3 ) ^ { 2 } = 0 $, 所以 $ 2 m - 1 = 0 , n - 3 = 0 $, 所以 $ m = \frac { 1 } { 2 } , n = 3 $。
当 $ m = \frac { 1 } { 2 } , n = 3 $ 时, 原式 $ = 2 × \frac { 1 } { 2 } + 3 - 4 = 0 $。
因为 $ | 2 m - 1 | + ( n - 3 ) ^ { 2 } = 0 $, 所以 $ 2 m - 1 = 0 , n - 3 = 0 $, 所以 $ m = \frac { 1 } { 2 } , n = 3 $。
当 $ m = \frac { 1 } { 2 } , n = 3 $ 时, 原式 $ = 2 × \frac { 1 } { 2 } + 3 - 4 = 0 $。
16. 如图,某市有一块长为$(3a+b)m$、宽为$(2a+b)m$的长方形地块,规划部门计划将阴影部分进行绿化,中间修建一座雕像,左右两边修两条宽为$am的道路(a>0,b>0)$。
(1)试用含$a$,$b$的代数式表示绿化面积;
(2)若$a= 3$,$b= 2$,求出绿化面积。
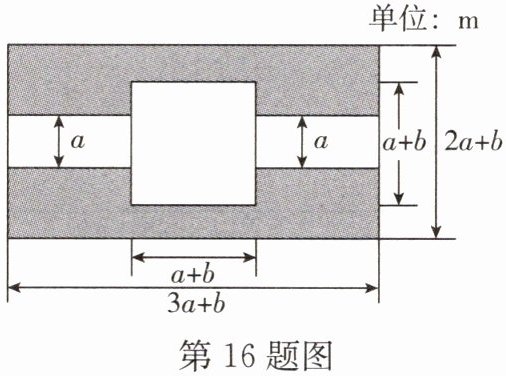
(1)试用含$a$,$b$的代数式表示绿化面积;
(2)若$a= 3$,$b= 2$,求出绿化面积。

答案:
解:
(1) $ ( 3 a + b ) ( 2 a + b ) - a [ 3 a + b - ( a + b ) ] - ( a + b ) ^ { 2 } $
$ = 6 a ^ { 2 } + 3 a b + 2 a b + b ^ { 2 } - a \cdot 2 a - a ^ { 2 } - 2 a b - b ^ { 2 } $
$ = 3 a ^ { 2 } + 3 a b $,
所以绿化面积为 $ ( 3 a ^ { 2 } + 3 a b ) \mathrm { m } ^ { 2 } $。
(2) 当 $ a = 3 , b = 2 $ 时,
绿化面积 $ = 3 × 3 ^ { 2 } + 3 × 3 × 2 = 45 ( \mathrm { m } ^ { 2 } ) $。
(1) $ ( 3 a + b ) ( 2 a + b ) - a [ 3 a + b - ( a + b ) ] - ( a + b ) ^ { 2 } $
$ = 6 a ^ { 2 } + 3 a b + 2 a b + b ^ { 2 } - a \cdot 2 a - a ^ { 2 } - 2 a b - b ^ { 2 } $
$ = 3 a ^ { 2 } + 3 a b $,
所以绿化面积为 $ ( 3 a ^ { 2 } + 3 a b ) \mathrm { m } ^ { 2 } $。
(2) 当 $ a = 3 , b = 2 $ 时,
绿化面积 $ = 3 × 3 ^ { 2 } + 3 × 3 × 2 = 45 ( \mathrm { m } ^ { 2 } ) $。
查看更多完整答案,请扫码查看


