《2025年暑假作业安徽教育出版社七年级数学北师大版》

11. 任意画一个角,作这个角的平分线,在角平分线上任取一点,作出这个点到角两边的距离,并量一量这两个距离的长短。再取一点,按上述步骤操作,你会得出什么结论？

答案： 解:角平分线上的点到角两边的距离相等。

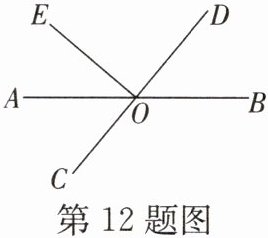
12. 如图,直线$AB与CD相交于点O$,射线$OE在∠AOD$的内部,$∠AOC= 70^{\circ}-\frac{1}{2}∠AOE$。当$∠AOE= 40^{\circ}$时,写出与$∠BOD$互余的角,并说明理由。

答案： 解:$ \angle AOE $与$ \angle BOD $互为余角。理由如下:
因为$ \angle AOC = 70 ^ { \circ } - \frac { 1 } { 2 } \angle AOE $，$ \angle AOE = 40 ^ { \circ } $，
所以$ \angle AOC = 70 ^ { \circ } - \frac { 1 } { 2 } × 40 ^ { \circ } = 50 ^ { \circ } $，
所以$ \angle BOD = \angle AOC = 50 ^ { \circ } $，
所以$ \angle BOD + \angle AOE = 50 ^ { \circ } + 40 ^ { \circ } = 90 ^ { \circ } $，
即$ \angle AOE $与$ \angle BOD $互为余角。

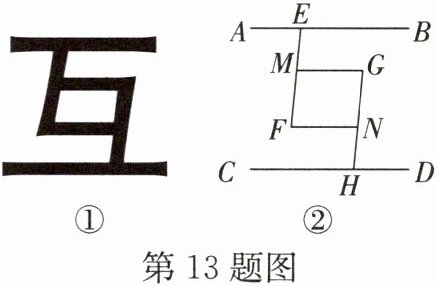
13. [跨学科融合]中国汉字博大精深,方块文字智慧灵秀,奥妙无穷。如图①所示的是一个“互”字,如图②所示的是由图①抽象的几何图形,其中$AB// CD$,$MG// FN$,点$E$,$M$,$F$在同一直线上,点$G$,$N$,$H$在同一直线上,且$∠EFN= ∠G$。
(1)$EF与GH$平行吗？理由是什么？
(2)试说明：$∠AEF= ∠GHD$。

答案：
解:
(1)平行。理由如下:
因为$ MG // FN $，所以$ \angle EFN = \angle EMG $。
因为$ \angle EFN = \angle G $，所以$ \angle G = \angle EMG $。所以$ EF // GH $。
(2)延长EF交CD于点P,如图所示。
因为$ AB // CD $，所以$ \angle BEF + \angle MPH = 180 ^ { \circ } $。
由
(1)得$ EP // GH $，
所以$ \angle GHP + \angle MPH = 180 ^ { \circ } $。所以$ \angle BEF = \angle GHP $。
因为$ \angle BEF = 180 ^ { \circ } - \angle AEF $，$ \angle GHP = 180 ^ { \circ } - \angle GHD $，所以$ \angle AEF = \angle GHD $。