《2025年暑假作业安徽教育出版社七年级数学北师大版》

13. 如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即$AE// CD$)。若$\angle A= 98^{\circ}$,$\angle B= 162^{\circ}$,则$\angle C$的度数是______。

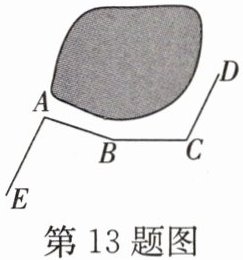
答案： $116^{\circ}$

14. 如图,在四边形ABCD中,$AD// BC$,$\angle B= \angle D$,点E在BA的延长线上,连接CE。
(1)试说明：$\angle E= \angle ECD$；
(2)若$\angle E= 60^{\circ}$,CE平分$\angle BCD$,直接写出$\triangle BCE$的形状。

答案： 解：
(1)因为$AD // BC$，所以$\angle EAD = \angle B$。
因为$\angle B = \angle D$，所以$\angle EAD = \angle D$，
所以$BE // CD$，所以$\angle E = \angle ECD$。
(2)$\triangle BCE$是等边三角形。

15. 如图,$AB// CD$,分别探讨下面4个图形中$\angle APC与\angle PAB$,$\angle PCD$的关系,请你从所得到的关系中任选一个加以说明。(可适当添加辅助线)

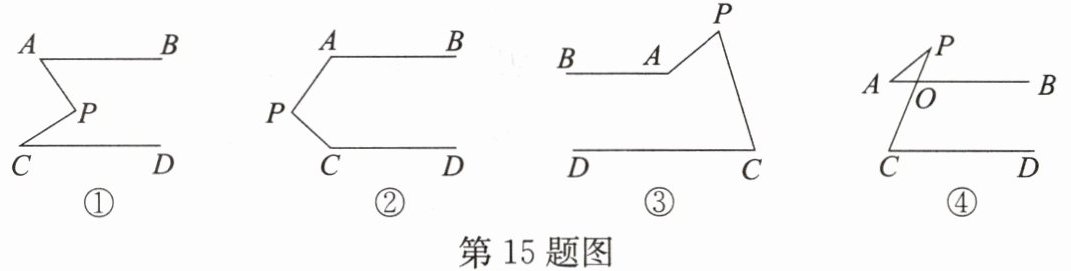
答案：
解：在图①中，$\angle APC = \angle PAB + \angle PCD$。

在图②中，$\angle APC + \angle PAB + \angle PCD = 360^{\circ}$。
在图③中，$\angle APC = \angle PAB - \angle PCD$。
在图④中，$\angle APC = \angle PCD - \angle PAB$。
证明图①中的关系式。
理由如下：如图①，过点$P$作$PF // AB$。
又因为$AB // CD$，所以$AB // CD // PF$，
所以$\angle APF = \angle PAB$，$\angle CPF = \angle PCD$，
所以$\angle APC = \angle PAB + \angle PCD$。