第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
三、按要求画图。
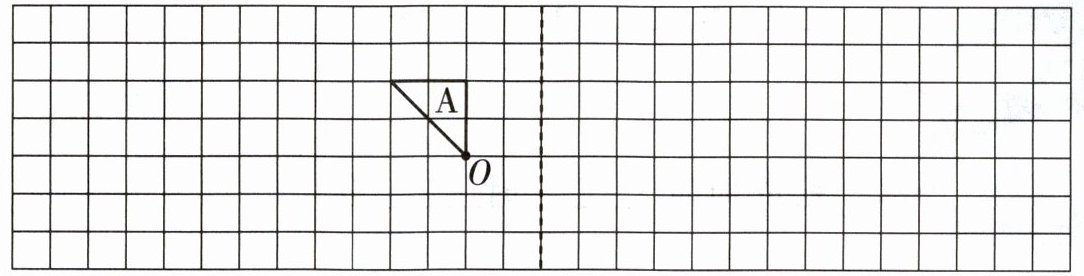
1. 以虚线为对称轴,画出图形 A 的轴对称图形 B。
2. 画出图形 A 绕点 O 逆时针旋转 $ 90^\circ $后的图形 C。

1. 以虚线为对称轴,画出图形 A 的轴对称图形 B。
2. 画出图形 A 绕点 O 逆时针旋转 $ 90^\circ $后的图形 C。
答案:

四、有一种长方体包装箱,尺寸如图所示。
1. 做这个包装箱至少需要多少平方分米的硬纸板?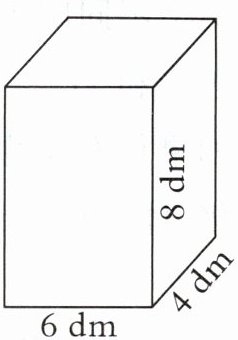
2. 这种包装箱能容纳物体的体积是多少立方分米? (厚度忽略不计)
1. 做这个包装箱至少需要多少平方分米的硬纸板?

2. 这种包装箱能容纳物体的体积是多少立方分米? (厚度忽略不计)
答案:
1. 解:$(8×6 + 8×4 + 6×4)×2$
$=(48 + 32 + 24)×2$
$=104×2$
$=208(dm^{2})$
2. 解:$6×8×4 = 192(dm^{3})$
$=(48 + 32 + 24)×2$
$=104×2$
$=208(dm^{2})$
2. 解:$6×8×4 = 192(dm^{3})$
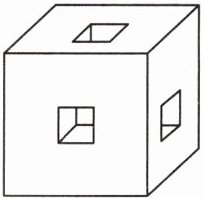
数学课上,老师带来一个玩具,这个玩具是由一个边长为 4 cm 的正方体分别在前后、左右、上下各面的中心位置挖去一个棱长为 1 cm 的小正方体做成的(如图)。老师让全班同学动脑筋,看谁能用最好的方法、最快地把这个玩具的表面积求出来。
你能求出这个玩具的表面积吗?
你能求出这个玩具的表面积吗?

答案:
大正方体的表面积:$4×4×6=96(cm^{2})$
每个小正方体增加的表面积:$1×1×4=4(cm^{2})$
6个小正方体共增加的表面积:$4×6=24(cm^{2})$
这个玩具的表面积:$96+24=120(cm^{2})$
答:这个玩具的表面积是$120cm^{2}$。
每个小正方体增加的表面积:$1×1×4=4(cm^{2})$
6个小正方体共增加的表面积:$4×6=24(cm^{2})$
这个玩具的表面积:$96+24=120(cm^{2})$
答:这个玩具的表面积是$120cm^{2}$。
查看更多完整答案,请扫码查看


