第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
1. 在括号里填上适当的体积或容积单位。
(1)一个脸盆约盛水6(
(3)一杯水约300(
(1)一个脸盆约盛水6(
L
)。 (2)一块橡皮的体积约8($ cm^{3} $
)。(3)一杯水约300(
mL
)。 (4)芳芳卧室的空间约48($ m^{3} $
)。
答案:
1.
(1) L
(2) $ cm^{3} $
(3) mL
(4) $ m^{3} $
(1) L
(2) $ cm^{3} $
(3) mL
(4) $ m^{3} $
2. 一个数的最大因数和最小倍数相加等于12,这个数是(
6
)。
答案:
一个数的最大因数是它本身,最小倍数也是它本身。设这个数为$x$,则$x + x = 12$,$2x = 12$,$x = 6$。
6
6
3. “红气球的个数是气球总数的$\frac {2}{3}$”,这里是把
气球总数
看作单位“1”,平均分成3
份,红气球的个数是这样的2
份。
答案:
气球总数 3 2
4. 6的倍数中最小的两位数是(
12
),28的因数中最大的一位数是(7
)。
答案:
6的倍数中最小的两位数是12,28的因数中最大的一位数是7。
5. 两个连续偶数的和是30,这两个数分别是(
14
)和(16
),它们的最小公倍数是(112
),最大公因数是(2
)。
答案:
解:设较小的偶数为$x$,则较大的偶数为$x + 2$。
$x + (x + 2) = 30$
$2x + 2 = 30$
$2x = 28$
$x = 14$
较大的偶数:$14 + 2 = 16$
14 的因数:1,2,7,14
16 的因数:1,2,4,8,16
最大公因数:2
14 的倍数:14,28,42,56,70,84,98,112,…
16 的倍数:16,32,48,64,80,96,112,…
最小公倍数:112
14;16;112;2
$x + (x + 2) = 30$
$2x + 2 = 30$
$2x = 28$
$x = 14$
较大的偶数:$14 + 2 = 16$
14 的因数:1,2,7,14
16 的因数:1,2,4,8,16
最大公因数:2
14 的倍数:14,28,42,56,70,84,98,112,…
16 的倍数:16,32,48,64,80,96,112,…
最小公倍数:112
14;16;112;2
6. 一根铁丝,剪去$\frac {2}{5}m$,剩下的比剪去的还多$\frac {2}{5}m$,这根铁丝原来长(
$1\frac{1}{5}$
)m。
答案:
解:剩下的长度为:$\frac{2}{5} + \frac{2}{5} = \frac{4}{5}$(m)
原来的长度 = 剪去的长度 + 剩下的长度,即$\frac{2}{5} + \frac{4}{5} = \frac{6}{5} = 1\frac{1}{5}$(m)
答:这根铁丝原来长$1\frac{1}{5}$m。
原来的长度 = 剪去的长度 + 剩下的长度,即$\frac{2}{5} + \frac{4}{5} = \frac{6}{5} = 1\frac{1}{5}$(m)
答:这根铁丝原来长$1\frac{1}{5}$m。
7.
从(
 )面看到的形状是
)面看到的形状是
,从左面看到的形状是( )。至少再添( )个相同的小正方体才能拼成一个从上面看是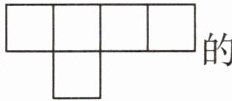
的几何体。
从(

 )面看到的形状是
)面看到的形状是,从左面看到的形状是( )。至少再添( )个相同的小正方体才能拼成一个从上面看是

的几何体。
答案:
7. 正 1
1
7. 正
 1
1 8. 把一个长16cm,宽6cm,高8cm的大长方体切成两个小长方体,这两个小长方体的表面积之和最大是(
800
)$cm^{2}$。
答案:
解:原长方体表面积:$2×(16×6 + 16×8 + 6×8) = 2×(96 + 128 + 48) = 2×272 = 544$($cm^2$)
要使表面积之和最大,增加的表面积应最大,即平行于最大面切割,最大面面积为$16×8 = 128$($cm^2$)
增加的表面积:$2×128 = 256$($cm^2$)
两个小长方体表面积之和:$544 + 256 = 800$($cm^2$)
答:800
要使表面积之和最大,增加的表面积应最大,即平行于最大面切割,最大面面积为$16×8 = 128$($cm^2$)
增加的表面积:$2×128 = 256$($cm^2$)
两个小长方体表面积之和:$544 + 256 = 800$($cm^2$)
答:800
二、计算下面各题,能简算的要简算。
$\frac {3}{4}+(\frac {1}{4}+\frac {7}{10})$ $\frac {4}{9}+\frac {5}{12}-\frac {5}{6}$ $\frac {5}{11}+\frac {3}{8}+\frac {9}{22}+\frac {5}{8}$
$\frac {3}{4}+(\frac {1}{4}+\frac {7}{10})$ $\frac {4}{9}+\frac {5}{12}-\frac {5}{6}$ $\frac {5}{11}+\frac {3}{8}+\frac {9}{22}+\frac {5}{8}$
答案:
$\frac{3}{4}+(\frac{1}{4}+\frac{7}{10})$
$=\frac{3}{4}+\frac{1}{4}+\frac{7}{10}$
$=1+\frac{7}{10}$
$=1\frac{7}{10}$
$\frac{4}{9}+\frac{5}{12}-\frac{5}{6}$
$=\frac{16}{36}+\frac{15}{36}-\frac{30}{36}$
$=\frac{31}{36}-\frac{30}{36}$
$=\frac{1}{36}$
$\frac{5}{11}+\frac{3}{8}+\frac{9}{22}+\frac{5}{8}$
$=(\frac{5}{11}+\frac{9}{22})+(\frac{3}{8}+\frac{5}{8})$
$=(\frac{10}{22}+\frac{9}{22})+1$
$=\frac{19}{22}+1$
$=1\frac{19}{22}$
$=\frac{3}{4}+\frac{1}{4}+\frac{7}{10}$
$=1+\frac{7}{10}$
$=1\frac{7}{10}$
$\frac{4}{9}+\frac{5}{12}-\frac{5}{6}$
$=\frac{16}{36}+\frac{15}{36}-\frac{30}{36}$
$=\frac{31}{36}-\frac{30}{36}$
$=\frac{1}{36}$
$\frac{5}{11}+\frac{3}{8}+\frac{9}{22}+\frac{5}{8}$
$=(\frac{5}{11}+\frac{9}{22})+(\frac{3}{8}+\frac{5}{8})$
$=(\frac{10}{22}+\frac{9}{22})+1$
$=\frac{19}{22}+1$
$=1\frac{19}{22}$
查看更多完整答案,请扫码查看


