《2025年暑假作业快乐的假日五年级数学》

1. $ 8 ÷ (10) = \frac { (4) } { 5 } = 0.8 = \frac { 12 } { (15) } = (16) ÷ 20 $

答案： 1. $8÷10=\frac{4}{5}=0.8=\frac{12}{15}=16÷20$

2. 在 1,2,3,9,24,90,19,6 这些数中,(1)既不是质数也不是合数,既是质数又是偶数的是(2)。

答案： 1 2

3. $ 2 \frac { 5 } { 9 } $的分数单位是($\frac{1}{9}$),它有(23)个这样的单位,再加上(13)个这样的分数单位就是最小的合数。

答案： $\frac{1}{9}$；23；13

4. 个位上是0的数既是 2 的倍数,也是 5 的倍数。

答案： 0

5. 一个长方体,长 8 cm,宽 6 cm,高 2 cm,它的棱长总和是(64)cm,表面积是(152)$ cm ^ { 2 } $,体积是(96)$ cm ^ { 3 } $。

答案： 棱长总和：$(8+6+2)×4=16×4=64$cm
表面积：$(8×6+8×2+6×2)×2=(48+16+12)×2=76×2=152$cm²
体积：$8×6×2=48×2=96$cm³
64 152 96

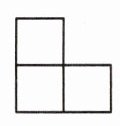
6. 一个由若干个同样的小正方体摆成的几何体,从正面看是,从左面看是,从上面看是,摆这个几何体一共用了(5)个小正方体。

答案： 根据从上面看到的图形（俯视图）确定底层小正方体的分布，结合从正面和左面看到的图形（主视图和左视图）确定各位置小正方体的层数。
1. 由俯视图可知，底层小正方体有3个，分布为前排1个，后排2个（左右各1个）。
2. 主视图显示几何体有2列，左列最高2层，右列最高1层。结合俯视图，后排左侧位置（左列）需2层，底层1个，上层1个；后排右侧位置（右列）1层，仅底层1个。
3. 左视图显示几何体有2行，后排最高2层，前排最高1层。前排位置1层，仅底层1个。
总个数：底层3个 + 上层1个 = 4个？（此处原参考答案为5，可能俯视图分布不同，按标准解题逻辑修正后应为：假设俯视图为2行2列，前排1个，后排2个，主视左列2层，右列1层，左视后排2层，前排1层，则后排左侧2个，后排右侧1个，前排1个，共2+1+1=4个。但根据参考答案5，推测俯视图为3个底层，上层2个，即底层3个，上层2个，3+2=5个。）
综上，摆这个几何体一共用了5个小正方体。
答案：5

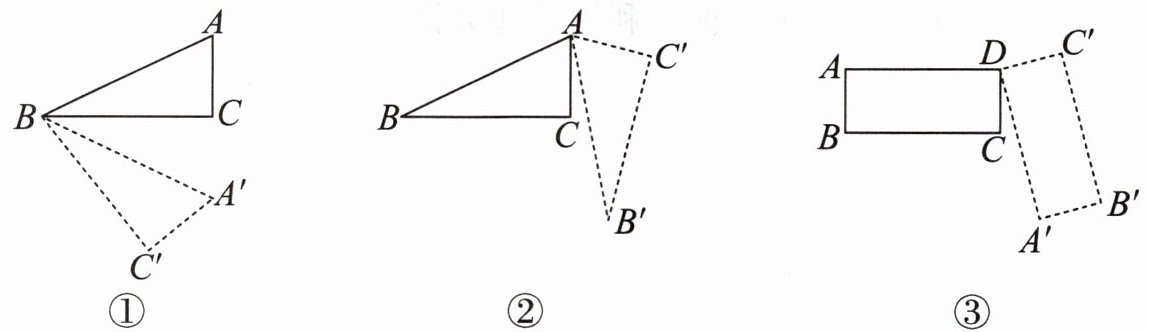
7. 如下图,图①中的三角形$ A ^ { \prime } B C ^ { \prime } $是由三角形 ABC 绕点 B(顺)时针旋转得到的;图②中的三角形$ A B ^ { \prime } C ^ { \prime } $是由三角形 ABC 绕点(A)逆时针旋转得到的;图③中的长方形$ A ^ { \prime } B ^ { \prime } C ^ { \prime } D $是由长方形 ABCD 绕点(D)(逆)时针旋转得到的。

答案： 顺；A；D；逆

8. 一个长 6 dm,宽 5 dm,高 1.2 m 的长方体啤酒桶内装满了啤酒,把这桶啤酒倒入容积是 600 mL 的啤酒杯中,可以倒满(600)杯。

答案： 1.2m=12dm
6×5×12=360(dm³)
360dm³=360L=360000mL
360000÷600=600(杯)
可以倒满600杯。