《2025年暑假作业快乐的假日五年级数学》

1. 在括号里填上合适的体积或容积单位。
(1)一盒牛奶约有 250(mL)。 (2)微波炉的体积约是 46($dm^{3}$)。
(3)教室的空间约是 180($m^{3}$)。 (4)香皂的体积约是 40($cm^{3}$)。

答案：
(1)mL
(2)$dm^{3}$
(3)$m^{3}$
(4)$cm^{3}$

2. 在 10~20 各数中,偶数有10,12,14,16,18,20,奇数有11,13,15,17,19,质数有11,13,17,19,合数有10,12,14,15,16,18,20,既是奇数又是合数的有15。

答案： 在10~20各数中，偶数有(10,12,14,16,18,20)，奇数有(11,13,15,17,19)，质数有(11,13,17,19)，合数有(10,12,14,15,16,18,20)，既是奇数又是合数的有
(15)。

3.
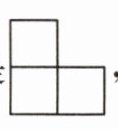
从(左)面看是
,从(上)面看是
。要使从左面看到的形状不变,添 1 个相同的小正方体,有(8)种不同的添法。

答案： 左 上 8

4. 在$◯$里填上“＞”“＜”或“=”。
$2\frac{1}{4}◯\frac{9}{4}$ = $\frac{3}{4}◯\frac{4}{5}$ ＜ $\frac{15}{4}◯3\frac{2}{5}$ ＞ $\frac{7}{16}◯0.5$ ＜
$30÷45◯\frac{2}{3}$ = $\frac{3}{7}◯\frac{3}{5}$ ＜ $0.29◯\frac{7}{25}$ ＞ $5\frac{1}{4}◯\frac{21}{4}$ =

答案： $2\frac{1}{4}=\frac{9}{4}$，所以$2\frac{1}{4}= \frac{9}{4}$；
$\frac{3}{4}=\frac{15}{20}$，$\frac{4}{5}=\frac{16}{20}$，$\frac{15}{20}＜\frac{16}{20}$，所以$\frac{3}{4}＜\frac{4}{5}$；
$\frac{15}{4}=3\frac{3}{4}=3\frac{15}{20}$，$3\frac{2}{5}=3\frac{8}{20}$，$3\frac{15}{20}＞3\frac{8}{20}$，所以$\frac{15}{4}＞3\frac{2}{5}$；
$\frac{7}{16}=0.4375$，$0.4375＜0.5$，所以$\frac{7}{16}＜0.5$；
$30÷45=\frac{30}{45}=\frac{2}{3}$，所以$30÷45= \frac{2}{3}$；
分子相同，分母小的分数大，$7＞5$，所以$\frac{3}{7}＜\frac{3}{5}$；
$\frac{7}{25}=0.28$，$0.29＞0.28$，所以$0.29＞ \frac{7}{25}$；
$5\frac{1}{4}=\frac{21}{4}$，所以$5\frac{1}{4}= \frac{21}{4}$。
= ＜ ＞ ＜ = ＜ ＞ =

5. 如图,将边长为 1 cm 的小正方体搭成的立体图形堆放在墙角,这个立体图形露在外面的面积是(18)$cm^{2}$,至少还需要(17)个这样的小正方体才能搭成一个大正方体。

答案： 解：小正方体一个面的面积为$1×1 = 1cm^{2}$。
从正面看，露在外面的小正方形个数为：$1 + 2 + 3 = 6$（个）；
从上面看，露在外面的小正方形个数为：$1 + 2 + 3 = 6$（个）；
从右面看，露在外面的小正方形个数为：$1 + 2 + 3 = 6$（个）。
露在外面的总面积为：$6 + 6 + 6 = 18cm^{2}$。
该立体图形底层有$3$个小正方体，中层有$2$个，上层有$1$个，总共有$3 + 2 + 1 = 6$个小正方体。
要搭成的大正方体棱长至少为$3cm$（因为底层已有$3$个小正方体排成一行），体积为$3×3×3 = 27$个小正方体体积。
至少还需要小正方体个数：$27 - 6 = 17$（个）。
18；17

6. 有 15 盒巧克力,其中 14 盒质量相同,另有 1 盒稍轻一些。如果用天平称,至少称(3)次才能保证找出这盒巧克力。

答案： 解：第一次，将15盒巧克力分成5、5、5三组，把其中两份5盒的分别放在天平两端。若天平平衡，则稍轻的在未称的5盒中；若不平衡，则稍轻的在天平上升一端的5盒中。
第二次，把有稍轻巧克力的5盒分成2、2、1三组，将两份2盒的放在天平两端。若天平平衡，则剩下的1盒就是稍轻的；若不平衡，则稍轻的在天平上升一端的2盒中。
第三次，把天平上升一端的2盒分别放在天平两端，上升一端的那盒就是稍轻的巧克力。
至少称3次才能保证找出这盒巧克力。
答案：3

1. 直接写出得数。
$\frac{1}{2}+\frac{1}{4}=$$\frac{3}{4}$ $\frac{3}{5}-\frac{1}{3}=$$\frac{4}{15}$ $\frac{5}{6}+\frac{1}{6}=$1 $\frac{2}{7}+\frac{3}{14}=$$\frac{1}{2}$
$8+\frac{2}{5}=$$8\frac{2}{5}$ $\frac{3}{8}-0.375=$0 $5-\frac{1}{3}=$$4\frac{2}{3}$ $3\frac{5}{12}-\frac{1}{6}=$$3\frac{1}{4}$

答案： 1. $\frac{3}{4}$；$\frac{4}{15}$；1；$\frac{1}{2}$；$8\frac{2}{5}$；0；$4\frac{2}{3}$；$3\frac{1}{4}$
 

2. 计算下面各题,能简算的要简算。
$\frac{7}{9}+(\frac{2}{9}-\frac{1}{18})$ $\frac{2}{3}+4\frac{5}{7}-(2\frac{5}{7}-1\frac{1}{3})$ $2.64-\frac{3}{4}+3.36-\frac{1}{4}$

答案： 2.
$\frac{7}{9}+(\frac{2}{9}-\frac{1}{18})$
$=\frac{7}{9}+\frac{2}{9}-\frac{1}{18}$
$=1-\frac{1}{18}$
$=\frac{17}{18}$
$\frac{2}{3}+4\frac{5}{7}-(2\frac{5}{7}-1\frac{1}{3})$
$=\frac{2}{3}+4\frac{5}{7}-2\frac{5}{7}+1\frac{1}{3}$
$=(\frac{2}{3}+1\frac{1}{3})+(4\frac{5}{7}-2\frac{5}{7})$
$=2+2$
$=4$
$2.64-\frac{3}{4}+3.36-\frac{1}{4}$
$=(2.64+3.36)-(\frac{3}{4}+\frac{1}{4})$
$=6-1$
$=5$