《2025年暑假作业快乐的假日五年级数学》

1. 这是一个长方体的展开图,求这个长方体的体积。

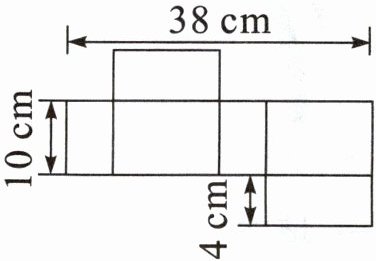
答案： 解：$(38 - 4×2)÷2 = 15(cm)$
$15×10×4 = 600(cm^{3})$
答：这个长方体的体积是$600cm^{3}$。

2. 求下面这个图形的表面积。(每个小正方体的棱长都是 2 cm)

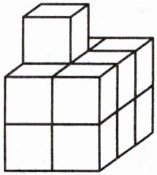
答案： 解：从不同方向观察该图形，前面和后面各有5个小正方形面，左面和右面各有7个小正方形面，上面和下面各有6个小正方形面。
总面数：$(5 + 7 + 6)×2 = 36$（个）
每个小正方形面的面积：$2×2 = 4(cm^{2})$
图形表面积：$36×4 = 144(cm^{2})$
答：该图形的表面积是$144cm^{2}$。

1. 甲、乙两人加工一批零件,甲单独加工需要 20 天能完成,乙单独加工需要 30 天能完成。如果甲、乙两人合作,那么一天可以加工这批零件的几分之几?

答案： 解：甲一天加工这批零件的$\frac{1}{20}$，乙一天加工这批零件的$\frac{1}{30}$。
两人合作一天加工零件的占比为：$\frac{1}{20} + \frac{1}{30}$
$=\frac{3}{60} + \frac{2}{60}$
$=\frac{5}{60}$
$=\frac{1}{12}$
答：甲、乙两人合作一天可以加工这批零件的$\frac{1}{12}$。

2. 测量一块不规则铁块的体积。实验小组的同学先将 5 L 水注入一个长方体水箱中(如图 1),然后再将这块不规则铁块放入这个长方体水箱中(如图 2),先后测量得到的数据如图所示。你能利用这些数据计算出不规则铁块的体积吗?

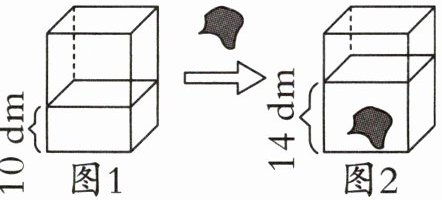
答案： $5L=5dm^{3}$
$5÷10×(14 - 10)=2(dm^{3})$
答：不规则铁块的体积是$2dm^{3}$。