第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
4. 下面的图形中(每个小方格都是正方形),()不是正方体的表面展开图。
A.
B.
C.
D.
A.
B.
C.
D.
答案:
C
5. 从一个体积是 $ 16 \mathrm{cm}^{3} $ 的长方体中,挖掉一个小正方体后(如图),它的表面积和原来相比,()。

A. 不变
B. 变小了
C. 变大了
D. 无法判断

A. 不变
B. 变小了
C. 变大了
D. 无法判断
答案:
A
三 计算下面各立体图形的表面积和体积。
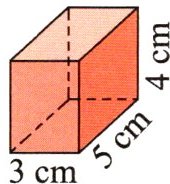
1.
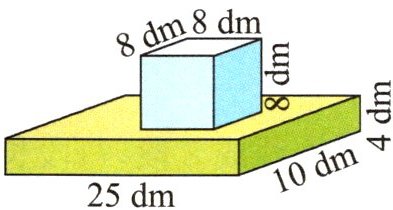
2.

1.
2.

答案:
1. 表面积:$(3×5+3×4+5×4)×2=94(cm^{2})$
体积:$3×5×4=60(cm^{3})$
2. 表面积:$(25×4+10×4+25×10)×2+8×8×4=1036(dm^{2})$
体积:$25×10×4+8×8×8=1512(dm^{3})$
体积:$3×5×4=60(cm^{3})$
2. 表面积:$(25×4+10×4+25×10)×2+8×8×4=1036(dm^{2})$
体积:$25×10×4+8×8×8=1512(dm^{3})$
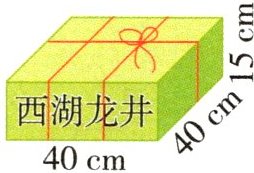
1. (生活体验)五月初,杭州各地茶农忙于采摘和售卖茶叶。聪聪家正在打包一个茶叶礼盒(如下图),打结处用了 $ 13 \mathrm{cm} $ 的绸带。
(1)打包这个茶叶礼盒至少需要用多长的绸带?
(2)如果把两盒包装在一起,最少需要多少平方分米的包装纸? (请先画出示意图,再解答)
我画的图: 我的解答:
(1)打包这个茶叶礼盒至少需要用多长的绸带?
(2)如果把两盒包装在一起,最少需要多少平方分米的包装纸? (请先画出示意图,再解答)
我画的图: 我的解答:

答案:
(1)$40×4+40×2+15×6+13=343(cm)$
(2)
$40×40×2+40×15×2×4=8000(cm^{2})$
$8000cm^{2}=80dm^{2}$
(1)$40×4+40×2+15×6+13=343(cm)$
(2)

$40×40×2+40×15×2×4=8000(cm^{2})$
$8000cm^{2}=80dm^{2}$
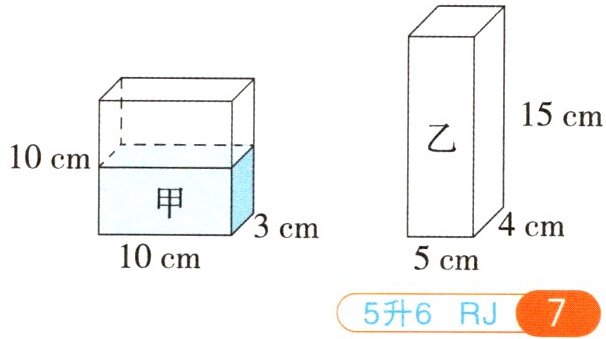
2. (空间观念)有甲、乙两个长方体形状的容器。甲容器的长、宽、高分别是 $ 10 \mathrm{cm} 、 3 \mathrm{cm} 、 10 \mathrm{cm} $,乙容器的长、宽、高分别是 $ 5 \mathrm{cm} 、 4 \mathrm{cm} 、 15 \mathrm{cm} $。已知甲容器中装有水,将其倾斜,水面刚好如下图所示。乙容器是空的。
(1)甲容器中水的体积是多少?
(2)如果将甲容器中的水倒一部分到乙容器中,使得甲、乙两个容器中的水面一样高,那么需要从甲容器中倒出多少体积的水?

(1)甲容器中水的体积是多少?
(2)如果将甲容器中的水倒一部分到乙容器中,使得甲、乙两个容器中的水面一样高,那么需要从甲容器中倒出多少体积的水?


答案:
(1)$10×3×10÷2=150(cm^{3})$
(2)$150÷(10×3+5×4)=3(cm)$
$5×4×3=60(cm^{3})$
(1)$10×3×10÷2=150(cm^{3})$
(2)$150÷(10×3+5×4)=3(cm)$
$5×4×3=60(cm^{3})$
查看更多完整答案,请扫码查看


