《2025年阳光同学暑假衔接五升六年级数学人教版》

例2 将一块长14cm、宽10cm、高3cm的长方体铁块完全浸没在一个长方体油箱中,取出铁块后,油面的高度下降了2.1cm。这个长方体油箱的底面积是多少平方厘米？
思路点拨

尝试解答
方法总结
根据题意,长方体铁块的体积等于下降的油的体积,先计算出长方体铁块的体积,再用下降的油的体积÷下降的高度= 油箱的底面积。

答案： $ 14 \times 10 \times 3 \div 2.1 = 200 ( \mathrm { cm } ^ { 2 } ) $

4.(仿例练习)

答案： $ ( 400 - 200 ) \div ( 6 - 1 ) = 40 ( \mathrm { mL } ) $
$ 40 \mathrm { mL } = 40 \mathrm { cm } ^ { 3 } $

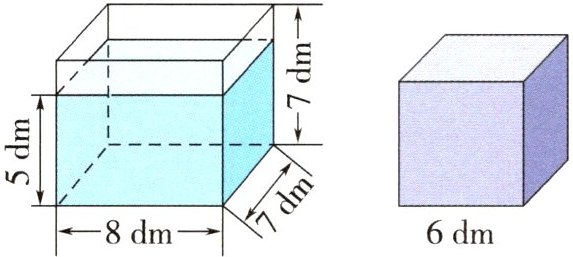
5.(变式提升)如图,一个长方体玻璃缸中水深5dm,将一块棱长是6dm的正方体铁块投入水中,玻璃缸里的水会溢出多少立方分米？

答案： $ 8 \times 7 \times ( 7 - 5 ) = 112 ( \mathrm { dm } ^ { 3 } ) $
$ 6 \times 6 \times 6 = 216 ( \mathrm { dm } ^ { 3 } ) $
$ 216 - 112 = 104 ( \mathrm { dm } ^ { 3 } ) $

6.(素养培优)如图,一个无水的观赏鱼缸中放着一块高为3dm、体积为$5dm^3$的假山石。现在需要向鱼缸中注水完全淹没假山石。
(1)至少需要多少升水？
(2)如果再放入一块高2dm、体积为$3.2dm^3$的假山石,那么水面会上升多少厘米？

答案：
(1)$ 8 \times 4 \times 3 - 5 = 91 ( \mathrm { dm } ^ { 3 } ) $
$ 91 \mathrm { dm } ^ { 3 } = 91 \mathrm { L } $
(2)$ 3.2 \div ( 8 \times 4 ) = 0.1 ( \mathrm { dm } ) $
$ 0.1 \mathrm { dm } = 1 \mathrm { cm } $