《2025年阳光同学暑假衔接五升六年级数学人教版》

4. 把一块正方体的橡皮泥捏成一个长方体后,下面的说法正确的是()。
A. 体积不变,表面积变小
B. 体积不变,表面积变大
C. 表面积不变,体积变小
D. 表面积不变,体积变大

答案： B

5. (空间观念)如图,分别用 8 个相同的小正方体测量 4 个盒子的容积,()中盒子的容积最大。

A. [img ]
B. [img ]
C. [img ]
D. [img ]

答案： B

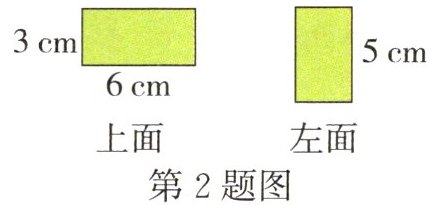
1. 如图所示为长方体表面展开图的一部分。(每个小方格表示$1cm^{2}$)
(1)请在虚线①、②的旁边将长方体的展开图补充完整。
(2)这个长方体的表面积是()$cm^{2}$,体积是()$cm^{3}$。

[img ]

答案：

(1)
(2)22 6

2. (说理表达)爸爸给林林买了一个 14 面的魔方,它是由 6 个正方形和 8 个三角形组成的。林林推断:“每个正方形有 4 条边,每个三角形有 3 条边,这个多面体应该有 48 条棱,算式为$6×4+8×3= 48$(条)。”你觉得他的想法正确吗? 请说明理由。
[img ]

答案： 不正确 示例:正方形和三角形有共同的边,没有去掉共同的边

1. (空间观念)有甲、乙两块形状不同的铁皮,现将每块铁皮(无剩余)分别沿虚线弯折后焊接成一个无盖且底面是正方形的长方体铁桶。哪个铁桶装水多一些?

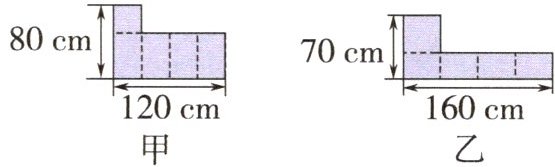
[img ]

答案： 甲铁桶:120÷4 = 30(cm) 80 - 30 = 50(cm) 30×30×50 = 45000(cm³)
乙铁桶:160÷4 = 40(cm) 70 - 40 = 30(cm) 40×40×30 = 48000(cm³)
45000 ＜ 48000,乙铁桶装水多一些

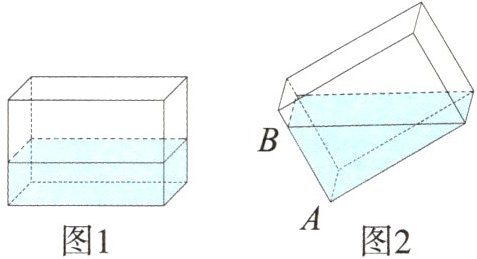
2. (福州期末真题)一个长 15 cm、宽 7.5 cm、高 10 cm 的长方体形状的玻璃缸里有一些水,水深 0.4 dm(如图 1)。
(1)这些水的体积是多少立方厘米?
(2)如果把玻璃缸的一边抬高(如图 2),那么这时 AB 长多少厘米?
[img ]
[img ]
[img ]

答案：
(1)0.4dm = 4cm 15×7.5×4 = 450(cm³)
(2)450×2÷(15×7.5) = 8(cm)