《2025年阳光同学暑假衔接五升六年级数学人教版》

2. (数学与科学)一个学习小组为了测量一块石头的体积,进行了如下实验。
步骤1:准备一个长方体形状的玻璃缸,并从里面测出长是20cm、宽是10cm、高是15cm。
步骤2:往玻璃缸中倒入1L的水。
步骤3:把这块石头放入玻璃缸中,发现石头被水淹没了,但没有水溢出。
步骤4:测出水面上升了2cm。
根据测量结果,这块石头的体积是多少立方厘米? 合多少立方分米?

答案： $20×10×2 = 400(cm^{3})$ $400cm^{3} = 0.4dm^{3}$

3. (说理表达)我们学习长方体表面积时,知道了长方体的表面积$=$(长$×宽+长×高+宽×$高)$×2$。在学习中乐乐发现:长方体的侧面积$=底面周长×$高,你觉得他的发现正确吗? 如果正确,那么请你结合下面的长方体和它的展开图,试着用文字或举例计算等方法说明理由。

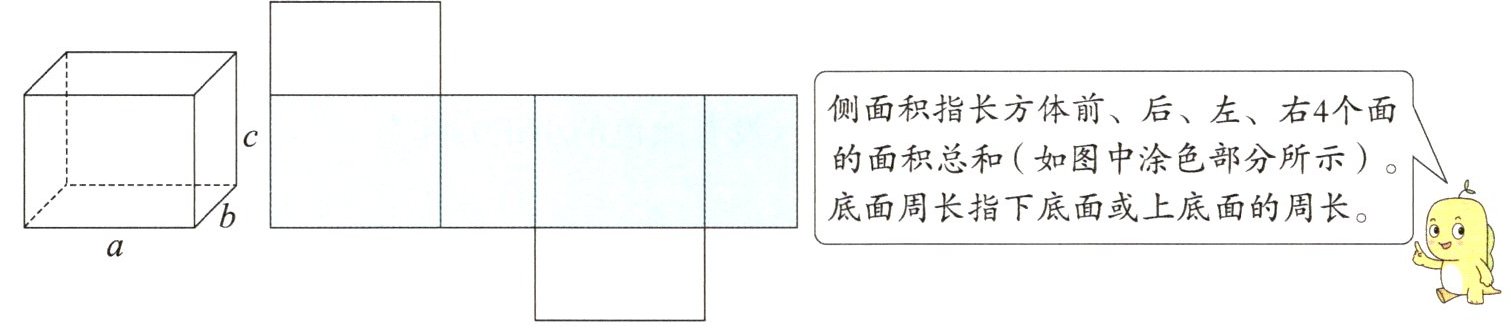
侧面积指长方体前、后、左、右4个面的面积总和(如图中涂色部分所示)。
底面周长指下底面或上底面的周长。

答案： 他的发现正确 示例：长方体的侧面展开图可以看成一个长方形，它的长等于长方体的底面周长，宽等于长方体的高，根据长方形的面积 = 长×宽，则长方体的侧面积 = 底面周长×高

4. (新题型)请阅读以下材料,再解决问题。
我们知道:“一个数各数位上数的和是3的倍数,这个数就是3的倍数”,例如123各数位上数的和是6,是3的倍数,所以123是3的倍数。为什么可以这样判断? 其实背后是有道理的。
根据数的意义,123是1个百、2个十、3个一组成的,它可以表示成:$123= 1×100+2×10+3$。100不是3的倍数,但是99是3的倍数,9也是3的倍数。根据乘法分配律:
$123&= 1×100+2×10+3&=1×(99+1)+2×(9+1)+3&=1×99+1+2×9+2+3\end{align}$
其中$1×99和2×9$一定是3的倍数,剩下只需要看“$1+2+3$”,也就是“各数位上数的和”是否为3的倍数便可以进行判断了。
(1)先判断下面各数是否为9的倍数(是的在后面画“√”),再在括号里写出9的倍数的特征。
903()
693()
239()
990()
(),这个数就是9的倍数。
(2)请根据阅读材料,解释判断一个数是不是9的倍数的方法的道理。

答案：
(1)693(√) 990(√) 一个数各数位上数的和是9的倍数
(2)示例：$6786 = 6×1000 + 7×100 + 8×10 + 6 = 6×(999 + 1) + 7×(99 + 1) + 8×(9 + 1) + 6 = 6×999 + 6 + 7×99 + 7 + 8×9 + 8 + 6 = (6×999 + 7×99 + 8×9) + 6 + 7 + 8 + 6$，括号里都是9的倍数，剩下部分刚好是各数位上数的和，即$6 + 7 + 8 + 6 = 27$，是9的倍数，所以一个数各数位上数的和是9的倍数，这个数就是9的倍数