《2025年高效课堂新疆青少年出版社五年级数学下册北师大版》

例:如图,包装一个长方体礼品盒,选择下面哪种尺寸的包装纸比较合适？(单位:cm)

答案：
将礼品盒展开后如右图:

长：$4\times2 + 6\times2 = 20(\text{cm})$
宽：$4\times2 + 10 = 18(\text{cm})$
所以包装纸尺寸至少为$20\times18$。
选用包装纸②比较合适。
解析：根据长方体展开图的特征计算展开图的长与宽，然后与两种包装纸的尺寸对比。

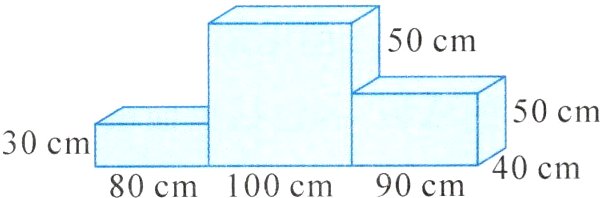
例:要给如图所示的领奖台除底面以外全部刷漆，需要刷漆的部分面积是多少？

第二单元重难点训练
提升训练

答案：
正面面积：$80\times30 + 100\times(50 + 50)+90\times50 = 16900(\text{cm}^2)$，右面面积：$40\times(50 + 50)=4000(\text{cm}^2)$，上面面积：$40\times(80 + 100 + 90)=10800(\text{cm}^2)$，刷漆部分面积：$16900\times2 + 4000\times2 + 10800 = 52600(\text{cm}^2)$。解析：求实际问题中的面积时，先确定面的个数，面与面之间的关系，再按不同方向逐个求面积，做到不重不漏。

1. 选择题。
(1) 包装如下图所示的长方体纸盒，应选择(　　　)尺寸的包装纸。(单位:cm)

A. $15\times16$
B. $35\times5$
C. $25\times12$

答案： 第二单元重难点训练
1.
(1) A 

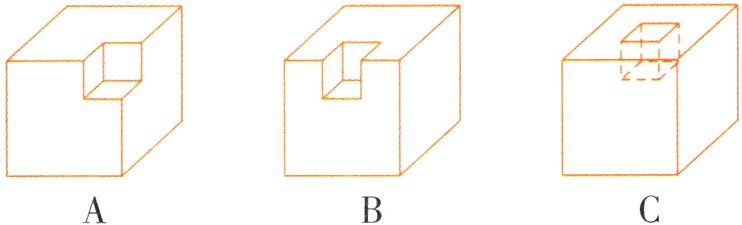
(2) 如图，在棱长为$8\text{ cm}$的大正方体上挖去一个棱长为$2\text{ cm}$的小正方体后，其表面积比原来多$16\text{ cm}^2$的挖法是(　　　)。

答案：
(2) C

2. 下图是一个长方体的展开图，围成一个这样的长方体框架需要多长的铁丝？

答案： $18 - 2 - 2 = 14(\text{cm})$
$(14 + 15 + 2)\times4 = 124(\text{cm})$
答：围成一个这样的长方体框架需要 124 cm 的铁丝。
解析：通过展开图可知道这个长方体的长是 15 cm，高是 2 cm，再用展开图的宽减去两条高，就得到这个长方体的宽，由此求出这个长方体的棱长总和，即围成这样一个长方体框架需要的铁丝长度。

3. 如下图，妈妈买了一个书架（有背板），书架外包装标明尺寸为$60\times40\times200$（单位：cm），制作这个书架至少需要木料多少平方分米？

答案： $60\times200 + 40\times200\times2 + 60\times40\times6$
$= 12000 + 16000 + 14400$
$= 28000 + 14400$
$= 42400(\text{cm}^2)$
$42400\text{ cm}^2 = 424\text{ dm}^2$
答：制作这个书架至少需要木料 424 dm²。