《2025年教材全练五年级数学下册人教版天津专版》

1. 填一填。
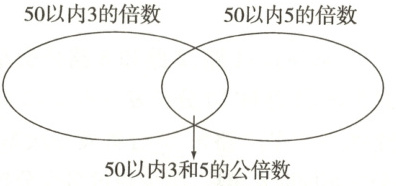
(1)50以内6的倍数有(　　　　　　　　　)。
50以内9的倍数有(　　　　　　　　　)。
50以内6和9的公倍数有(　　　　　　　)。
6和9的最小公倍数是(　　)。
(2) 
(3)如果m和n的最大公因数是1,那么m和n的最小公倍数是(　　　)。

答案：

(1)6,12,18,24,30,36,42,48
9,18,27,36,45 18,36 18
(2)
 
(3)$mn$

2. 写出下面每组数的最小公倍数。
(1)36和24
(2)22和33
(3)9和10
(4)19和57

答案：
(1)72
(2)66
(3)90
(4)57

3. 写出下面各组分数的两个分母的最小公倍数。
(1)$\frac{9}{13}$和$\frac{2}{39}$(　　　　)
(2)$\frac{2}{3}$和$\frac{1}{7}$(　　　　)
(3)$\frac{2}{9}$和$\frac{7}{12}$(　　　　)
(4)$\frac{8}{57}$和$\frac{15}{171}$(　　　　)

答案：
(1)39
(2)21
(3)36
(4)171
[解析]
(1)因为$39\div13 = 3$，所以13和39的最小公倍数是39。
(2)因为3和7是互质数，所以3和7的最小公倍数是$3\times7 = 21$。
(3)因为9的倍数有9,18,27,36,45…12的倍数有12,24,36,48…所以9和12的最小公倍数是36。
(4)因为$171\div57 = 3$，所以57和171的最小公倍数是171。

4. 选择。
(1)两个数的最大公因数是7,最小公倍数是28,这两个数是(　　　)。
A. 14和56
B. 7和28
C. 7和14
D. 7和21
(2)如果$x = 2×7×11,y = 2×5×11$,那么x和y的最小公倍数是(　　)。
A. 22
B. 35
C. 770
D. 2
(3)已知$a÷b = c$（a,b,c都是不为0的自然数）,则a和b的最小公倍数是(　　　)。
A. a
B. b
C. c
D. ab

答案：
(1)B
(2)C
(3)A
[解析]
(1)可以先逐一求出四个选项中两个数的最大公因数和最小公倍数，再进行判断。
(2)根据给出的条件可知，两个数相同的质因数是2和11，各自独有的质因数是7和5，这几个数的乘积就是$x$和$y$的最小公倍数，即$2\times11\times7\times5 = 770$。
(3)通过$a\div b = c(a,b,c$都是不为0的自然数)，可以判断出$a$是$b$的倍数，两个数成倍数关系，最小公倍数是其中较大的数，即$a$。

5. 因为厦门同安区地处东南沿海,又具备一定的海拔高度,昼夜温差大,所以这里种植的杨梅甜度高。洋洋摘了一些杨梅,2个2个地数,3个3个地数,4个4个地数,5个5个地数,6个6个地数,都剩1个,这些杨梅至少有多少个?

答案： 2,3,4,5,6的最小公倍数是60，$60 + 1 = 61$(个)，所以这些杨梅至少有61个。
[解析]根据题意可知，杨梅的个数应比2,3,4,5,6的最小公倍数多1，先求出2,3,4,5,6的最小公倍数，即60，再用60加1求出答案。

6. “孟春之月,盛德在木”。植树节到了,五年级的同学们去植树,已知总人数最接近200人,分组时,按3人一组、4人一组或5人一组分,都能恰好分完。五年级有多少人去植树?

答案： 180人
[解析]由题意可知，五年级去植树的总人数既能被3整除，也能被4和5整除，即五年级去植树的总人数是3,4和5的公倍数。它们的最小公倍数是$3\times4\times5 = 60$，据此可知3,4和5的公倍数有60,120,180,240…已知去植树的总人数最接近200人，因为60,120,180,240…中最接近200的是180，所以五年级有180人去植树。