《2025年单元双测全优测评卷九年级数学下册人教版》

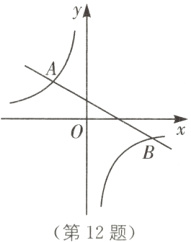
12.（2022·梧州中考）如图，在平面直角坐标系中，一次函数$y_1 = kx + b$的图象与反比例函数$y_2=\frac{m}{x}$的图象交于点A(-2,2)，B(n,-1). 当$y_1＜y_2$时，x的取值范围是_______.

答案： - 2＜x＜0或x＞4 [解析]
∵反比例函数y₂ = $\frac{m}{x}$的图象经过A( - 2,2)，
∴m = - 2×2 = - 4.
∴y = - $\frac{4}{x}$. 又反比例函数y = - $\frac{4}{x}$的图象经过B(n, - 1)，
∴n = 4.
∴B(4, - 1). 观察图象可知，当y₁＜y₂时，图中一次函数的函数值小于反比例函数的函数值，则x的取值范围为 - 2＜x＜0或x＞4.

13.（2023·陕西中考）如图，在矩形OABC和正方形CDEF中，点A在y轴正半轴上，点C，F均在x轴正半轴上，点D在边BC上，BC = 2CD，AB = 3. 若点B，E在同一个反比例函数的图象上，则这个反比例函数的表达式是_______.

答案： y = $\frac{18}{x}$ [解析]
∵四边形OABC是矩形，
∴OC = AB = 3.
∵四边形CDEF是正方形，
∴CD = CF = EF.
∵BC = 2CD，
∴设CD = m，BC = 2m，
∴B(3,2m)，E(3 + m,m). 设反比例函数的表达式为y = $\frac{k}{x}$，
∴3×2m = (3 + m)·m，解得m = 3或m = 0(不合题意舍去)，
∴B(3,6)，
∴k = 3×6 = 18，
∴这个反比例函数的表达式是y = $\frac{18}{x}$.

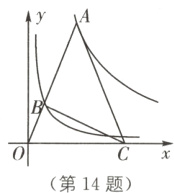
14. 如图，点A为函数$y=\frac{9}{x}(x＞0)$图象上一点，连接OA，交函数$y=\frac{1}{x}(x＞0)$的图象于点B，点C是x轴上一点，且AO = AC，则△ABC的面积为_______.

答案： 6 [解析]设A点的坐标为(a,$\frac{9}{a}$)，直线OA的解析式为y = kx，于是有$\frac{9}{a}$ = ka，
∴k = $\frac{9}{a²}$，直线OA的函数解析式为y = $\frac{9}{a²}$x，联立方程组$\begin{cases}y = \frac{9}{a²}x\\y = \frac{1}{x}\end{cases}$解得点B的坐标为($\frac{a}{3}$,$\frac{3}{a}$).
∵AO = AC，A(a,$\frac{9}{a}$)，
∴C(2a,0).
∴S△ABC = S△AOC - S△BOC = $\frac{1}{2}$×2a×$\frac{9}{a}$ - $\frac{1}{2}$×2a×$\frac{3}{a}$ = 9 - 3 = 6.

15.（2022·威海中考）正方形ABCD在平面直角坐标系中的位置如图所示，点A的坐标为(2,0)，点B的坐标为(0,4). 若反比例函数$y=\frac{k}{x}(k \neq 0)$的图象经过点C，则k的值为_______.

答案： 24

16. [跨学科综合]（2023·扬州中考）某气球内充满了一定质量的气体，在温度不变的条件下，气球内气体的压强p(Pa)是气球体积V(m³)的反比例函数，且当V = 3 m³时，p = 8 000 Pa. 当气球内的气体压强大于40 000 Pa时，气球将爆炸，为确保气球不爆炸，气球的体积应不小于_______m³.

答案： 0.6 [解析]设气球内气体的压强p(Pa)与气球体积V(m³)之间的函数解析式为p = $\frac{k}{V}$.
∵当V = 3 m³时，p = 8000 Pa，
∴k = Vp = 3×8000 = 24000，
∴p = $\frac{24000}{V}$，
∵气球内的气压大于40000 Pa时，气球将爆炸，
∴p≤40000时，气球不爆炸，
∴$\frac{24000}{V}$≤40000，解得V≥0.6，
∴为确保气球不爆炸，气球的体积应不小于0.6 m³.

17.（2022·宜宾中考）如图，△OMN是边长为10的等边三角形，反比例函数$y=\frac{k}{x}(x＞0)$的图象与边MN，OM分别交于点A，B（点B不与点M重合）. 若AB⊥OM于点B，则k的值为_______.

答案：
9$\sqrt{3}$ [解析]过点B作BC⊥x轴于点C，过点A作AD⊥x轴于点D，如图.

∵△OMN是边长为10的等边三角形，
∴OM = MN = ON = 10，∠MON = ∠MNO = ∠M = 60°.
∴∠OBC = ∠MAB = ∠NAD = 30°. 设OC = x，则OB = 2x，BC = $\sqrt{3}$x，MB = 10 - 2x，MA = 2MB = 20 - 4x，
∴NA = 10 - MA = 4x - 10，DN = $\frac{1}{2}$NA = 2x - 5，AD = $\sqrt{3}$DN = $\sqrt{3}$(2x - 5) = 2$\sqrt{3}$x - 5$\sqrt{3}$，
∴OD = ON - DN = 15 - 2x.
∴点B(x,$\sqrt{3}$x)，点A(15 - 2x,2$\sqrt{3}$x - 5$\sqrt{3}$).
∵反比例函数y = $\frac{k}{x}$(x＞0)的图象与边MN，OM分别交于点A，B，
∴x·$\sqrt{3}$x = (15 - 2x)(2$\sqrt{3}$x - 5$\sqrt{3}$)，解得x = 5(舍去)或x = 3，
∴点B(3,3$\sqrt{3}$)，
∴k = 9$\sqrt{3}$.

18. 如图，在平面直角坐标系中，O为坐标原点，□ABCD的边AB在x轴上，顶点D在y轴的正半轴上，点C在第一象限，将△AOD沿y轴翻折，使点A落在x轴上的点E处，点B恰好为OE的中点，DE与BC交于点F. 若$y=\frac{k}{x}(k \neq 0)$图象经过点C，且$S_{\triangle BEF}=1$，则k的值为_______.

答案：
24 [解析]过点F作FG⊥BE，FH⊥CD，垂足分别为G、H，如图.

设A( - 2a,0)，D(0,4b)，依题可得△ADO≌△EDO.
∴OA = OE.
∴E(2a,0).
∵B为OE中点，
∴B(a,0).
∴BE = a.
∵四边形ABCD是平行四边形，
∴AE//CD，AB = CD = 3a，C(3a,4b).
∴△CDF∽△BEF，
∴$\frac{HE}{GF}$ = $\frac{CD}{BE}$ = $\frac{1}{3}$，
∴FG = b. 又S△BEF = $\frac{1}{2}$BE·FG = 1，
∴$\frac{1}{2}$ab = 1.
∴ab = 2.
∵C(3a,4b)在反比例函数y = $\frac{k}{x}$上，
∴k = 3a·4b = 12ab = 12×2 = 24.