《2025年单元双测全优测评卷九年级数学下册人教版》

22.(8分)如图，为了测量一栋楼的高度$OE$，小明同学先在操场上$A$处放一面镜子，向后退到$B$处，恰好在镜子中看到楼的顶部$E$；再将镜子放到$C$处，然后后退到$D$处，恰好再次在镜子中看到楼的顶部$E$($O$，$A$，$B$，$C$，$D$在同一条直线上)，测得$AC = 2$ m，$BD = 2.1$ m，如果小明眼睛距地面高度$BF$，$DG$为1.6 m，试确定楼的高度$OE$.

答案： 设E关于O的对称点为M,延长GC,FA相交于点M,连接GF并延长交OE于点H，
　
∵GF//AC,
∴△MAC∽△MFG.
　
∴$\frac{AC}{FG}=\frac{MA}{MF}=\frac{MO}{MH}$,
　　即$\frac{AC}{BD}=\frac{OE}{MH}=\frac{OE}{MO + OH}=\frac{OE}{OE + BF}$,
　
∴$\frac{OE}{OE + 1.6}=\frac{2}{2.1}$.
∴OE = 32m.
　　故楼的高度OE为32m.

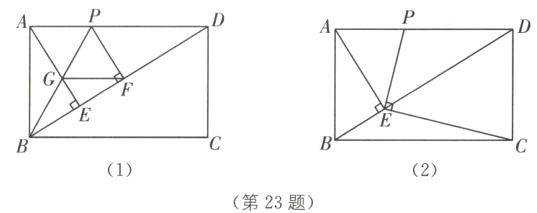
23.(8分)在矩形$ABCD$中，$AE\perp BD$于点$E$，点$P$是边$AD$上一点.
(1)若$BP$平分$\angle ABD$，交$AE$于点$G$，$PF\perp BD$于点$F$，如图(1)，证明四边形$AGFP$是菱形；
(2)若$PE\perp EC$，如图(2)，求证：$AE\cdot AB = DE\cdot AP$；
(3)在(2)的条件下，若$AB = 1$，$BC = 2$，求$AP$的长.

答案：
(1)
∵四边形ABCD是矩形，
　
∴∠BAD = 90°.
　
∵AE⊥BD,
∴∠AED = 90°.
　
∴∠BAE + ∠EAD = 90°,∠EAD + ∠ADE = 90°.
∴∠BAE = ∠ADE.
　
∵BP平分∠ABD,
∴∠ABP = ∠PBD.
　
∵∠AGP = ∠BAG + ∠ABG,∠APG = ∠ADE + ∠PBD,∠ABG = ∠PBD,
　
∴∠AGP = ∠APG.
∴AP = AG.
　
∵PA⊥AB,PF⊥BD,BP平分∠ABD,
　
∴PA = PF.
∴PF = AG.
　
∵AE⊥BD,PF⊥BD,
∴PF//AG.
　
∴四边形AGFP是平行四边形.
　
∵PA = PF,
∴四边形AGFP是菱形.
(2)
∵AE⊥BD,PE⊥EC,
　
∴∠AED = ∠PEC = 90°.
　
∴∠AEP = ∠DEC.
　
∵∠EAD + ∠ADE = 90°,∠ADE + ∠CDE = 90°,
∴∠EAP = ∠EDC.
　
∴△AEP∽△DEC.
∴$\frac{AE}{DE}=\frac{AP}{DC}$.
　
∵AB = CD,
∴AE·AB = DE·AP.
(3)
∵四边形ABCD是矩形，
　
∴BC = AD = 2,∠BAD = 90°.
　
∴BD = $\sqrt{AB^2 + AD^2}=\sqrt{5}$.
　
∵AE⊥BD,
∴$S_{\triangle ABD}=\frac{1}{2}BD\cdot AE=\frac{1}{2}AB\cdot AD$.
∴AE = $\frac{2\sqrt{5}}{5}$.
　
∴DE = $\sqrt{AD^2 - AE^2}=\frac{4\sqrt{5}}{5}$.
　
∵AE·AB = DE·AP,
　
∴AP = $\frac{\frac{2\sqrt{5}}{5}×1}{\frac{4\sqrt{5}}{5}}=\frac{1}{2}$.

24.(10分)［开放探究性问题］(2023·黄冈中考)［问题呈现］$\triangle CAB$和$\triangle CDE$都是直角三角形，$\angle ACB=\angle DCE = 90^{\circ}$，$CB = mCA$，$CE = mCD$，连接$AD$，$BE$，探究$AD$，$BE$的位置关系.

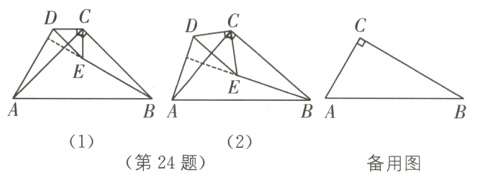
(1)如图(1)，当$m = 1$时，直接写出$AD$，$BE$的位置关系：_______；
(2)如图(2)，当$m\neq1$时，(1)中的结论是否成立？若成立，给出证明；若不成立，说明理由.
［拓展应用］
(3)当$m = \sqrt{3}$，$AB = 4\sqrt{7}$，$DE = 4$时，将$\triangle CDE$绕点$C$旋转，使$A$，$D$，$E$三点恰好在同一直线上，求$BE$的长.

答案：
(1)BE⊥AD
(2)成立.理由如下:
如图
(2),设BE的延长线交AD于点G.
∵∠DCE = ∠ACB = 90°,
∴∠DCA + ∠ACE = ∠ACE + ∠ECB = 90°,
∴∠DCA = ∠ECB.
∵$\frac{DC}{CE}=\frac{AC}{BC}=\frac{1}{m}$,
∴△DCA∽△ECB,
∴∠DAC = ∠CBE.
∵∠GAB + ∠ABG = ∠DAC + ∠CAB + ∠ABG = ∠CBE + ∠CAB + ∠ABG = ∠CAB + ∠CBA = 180° - ∠ACB = 90°,
∴∠AGB = 180° - 90° = 90°,
∴BE⊥AD.
(3)如图
(3),当点E在线段AD上时,连接BE.
设AE = x,则AD = AE + DE = x + 4,
根据解析
(2)可知△DCA∽△ECB,
∴$\frac{BE}{AD}=\frac{BC}{AC}=m=\sqrt{3}$,
∴BE = $\sqrt{3}AD=\sqrt{3}(x + 4)=\sqrt{3}x + 4\sqrt{3}$.
根据解析
(2)可知BE⊥AD，
∴∠AEB = 90°.
根据勾股定理，得$AE^2 + BE^2 = AB^2$，
即$x^2 + (\sqrt{3}x + 4\sqrt{3})^2=(4\sqrt{7})^2$，
解得x = 2或x = - 8(舍去)，
∴此时BE = $\sqrt{3}x + 4\sqrt{3}=6\sqrt{3}$；
如图
(4),当点D在线段AE上时,连接BE.
设AD = y,则AE = AD + DE = y + 4,
根据解析
(2)可知△DCA∽△ECB，
∴$\frac{BE}{AD}=\frac{BC}{AC}=m=\sqrt{3}$，
　
∴BE = $\sqrt{3}AD=\sqrt{3}y$，
　　根据解析
(2)可知BE⊥AD，
　
∴∠AEB = 90°，
　　根据勾股定理,得$AE^2 + BE^2 = AB^2$，
　　即$(y + 4)^2 + (\sqrt{3}y)^2=(4\sqrt{7})^2$，
　　解得y = 4或y = - 6(舍去),
　
∴此时BE = $\sqrt{3}y = 4\sqrt{3}$
　　综上所述,BE = $6\sqrt{3}$或$4\sqrt{3}$