2025年单元双测全优测评卷九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
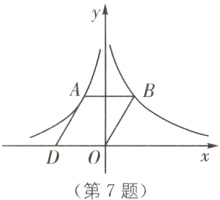
7.(2022·黑龙江中考)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数$y=\frac{3}{x}$的图象上,顶点A在反比例函数$y=\frac{k}{x}$的图象上,顶点D在x轴的负半轴上. 若平行四边形OBAD的面积是5,则k的值是( ).
A. 2
B. 1
C. -1
D. -2

A. 2
B. 1
C. -1
D. -2
答案:
D [解析]连接OA,设AB交y轴于点C.
∵四边形OBAD是平行四边形,平行四边形OBAD的面积是5,
∴S△AOB = $\frac{1}{2}$S▱OBAD = $\frac{5}{2}$.
∵AB//OD,
∴AB⊥y轴.
∵点B在反比例函数y = $\frac{3}{x}$的图象上,顶点A在反比例函数y = $\frac{k}{x}$的图象上,
∴S△COB = $\frac{3}{2}$,S△COA = - $\frac{k}{2}$,
∴S△AOB = S△COB + S△COA = $\frac{3}{2}$ - $\frac{k}{2}$ = $\frac{5}{2}$,解得k = - 2. 故选D.
∵四边形OBAD是平行四边形,平行四边形OBAD的面积是5,
∴S△AOB = $\frac{1}{2}$S▱OBAD = $\frac{5}{2}$.
∵AB//OD,
∴AB⊥y轴.
∵点B在反比例函数y = $\frac{3}{x}$的图象上,顶点A在反比例函数y = $\frac{k}{x}$的图象上,
∴S△COB = $\frac{3}{2}$,S△COA = - $\frac{k}{2}$,
∴S△AOB = S△COB + S△COA = $\frac{3}{2}$ - $\frac{k}{2}$ = $\frac{5}{2}$,解得k = - 2. 故选D.
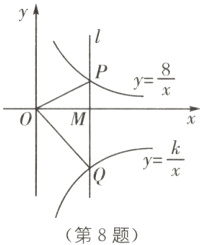
8.(2022·内江中考)如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l//y轴,且直线l分别与反比例函数$y=\frac{8}{x}$和$y=\frac{k}{x}$的图象交于P,Q两点. 若$S_{\triangle POQ}=15$,则k的值为( ).
A. 38
B. 22
C. -7
D. -22

A. 38
B. 22
C. -7
D. -22
答案:
D [解析]设点P(a,b),Q(a,$\frac{k}{a}$),则OM = a,PM = b,MQ = - $\frac{k}{a}$,
∴PQ = PM + MQ = b - $\frac{k}{a}$.
∵点P在反比例函数y = $\frac{8}{x}$的图象上,
∴ab = 8.
∵S△POQ = 15,
∴$\frac{1}{2}$PQ·OM = 15,
∴$\frac{1}{2}$a(b - $\frac{k}{a}$) = 15.
∴ab - k = 30,
∴8 - k = 30,解得k = - 22. 故选D.
∴PQ = PM + MQ = b - $\frac{k}{a}$.
∵点P在反比例函数y = $\frac{8}{x}$的图象上,
∴ab = 8.
∵S△POQ = 15,
∴$\frac{1}{2}$PQ·OM = 15,
∴$\frac{1}{2}$a(b - $\frac{k}{a}$) = 15.
∴ab - k = 30,
∴8 - k = 30,解得k = - 22. 故选D.
9. 已知点P(-3,2),点Q(2,a)都在反比例函数$y=\frac{k}{x}(k \neq 0)$的图象上,过点Q分别作两坐标轴的垂线,两垂线与两坐标轴围成的矩形面积为( ).
A. 3
B. 6
C. 9
D. 12
A. 3
B. 6
C. 9
D. 12
答案:
B
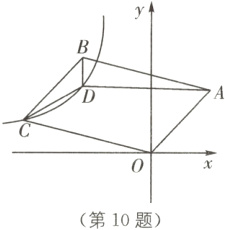
10.(2022·通辽中考)如图,点D是□OABC内一点,AD与x轴平行,BD与y轴平行,$BD=\sqrt{3}$,∠BDC = 120°,$S_{\triangle BCD}=\frac{9\sqrt{3}}{2}$,若反比例函数$y=\frac{k}{x}(x<0)$的图象经过C,D两点,则k的值是( ).
A. $-6\sqrt{3}$
B. -6
C. $-12\sqrt{3}$
D. -12

A. $-6\sqrt{3}$
B. -6
C. $-12\sqrt{3}$
D. -12
答案:
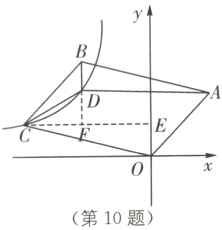
C [解析]过点C作CE⊥y轴于点E,延长BD交CE于点F,
∴∠CEO = 90°.
∵四边形OABC为平行四边形,
∴AB//OC,AB = OC.
∴∠COE = ∠ABD.
∵BD//y轴,AD//x轴,
∴∠ADB = ∠CEO = 90°.
∴△COE≌△ABD(AAS).
∴OE = BD = $\sqrt{3}$.
∵S△BDC = $\frac{1}{2}$BD·CF = $\frac{9}{2}\sqrt{3}$,
∴CF = 9.
∵∠BDC = 120°,
∴∠CDF = 60°.
∴DF = 3$\sqrt{3}$.
∴点D的纵坐标为4$\sqrt{3}$. 设C(m,$\sqrt{3}$),D(m + 9,4$\sqrt{3}$),
∵反比例函数y = $\frac{k}{x}$(x<0)的图象经过C,D两点,
∴k = $\sqrt{3}$m = 4$\sqrt{3}$(m + 9).
∴m = - 12.
∴k = - 12$\sqrt{3}$. 故选C.
C [解析]过点C作CE⊥y轴于点E,延长BD交CE于点F,
∴∠CEO = 90°.

∵四边形OABC为平行四边形,
∴AB//OC,AB = OC.
∴∠COE = ∠ABD.
∵BD//y轴,AD//x轴,
∴∠ADB = ∠CEO = 90°.
∴△COE≌△ABD(AAS).
∴OE = BD = $\sqrt{3}$.
∵S△BDC = $\frac{1}{2}$BD·CF = $\frac{9}{2}\sqrt{3}$,
∴CF = 9.
∵∠BDC = 120°,
∴∠CDF = 60°.
∴DF = 3$\sqrt{3}$.
∴点D的纵坐标为4$\sqrt{3}$. 设C(m,$\sqrt{3}$),D(m + 9,4$\sqrt{3}$),
∵反比例函数y = $\frac{k}{x}$(x<0)的图象经过C,D两点,
∴k = $\sqrt{3}$m = 4$\sqrt{3}$(m + 9).
∴m = - 12.
∴k = - 12$\sqrt{3}$. 故选C.
11.(2022·武汉中考)在反比例$y=\frac{k - 1}{x}$的图象的每一支上,y都随x的增大而减小,且整式$x^2 - kx + 4$是一个完全平方式,则该反比例函数的解析式为_______.
答案:
y = $\frac{3}{x}$ [解析]
∵x² - kx + 4是一个完全平方式,
∴ - k = ±4,即k = ±4.
∵在反比例函数y = $\frac{k - 1}{x}$的图象的每一支上,y都随x的增大而减小,
∴k - 1>0,
∴k>1. 解得k = 4.
∴反比例函数解析式为y = $\frac{3}{x}$.
方法诠释 利用完全平方公式的结构特征判断可求出k的值,再根据反比例函数的性质即可确定k的值.
∵x² - kx + 4是一个完全平方式,
∴ - k = ±4,即k = ±4.
∵在反比例函数y = $\frac{k - 1}{x}$的图象的每一支上,y都随x的增大而减小,
∴k - 1>0,
∴k>1. 解得k = 4.
∴反比例函数解析式为y = $\frac{3}{x}$.
方法诠释 利用完全平方公式的结构特征判断可求出k的值,再根据反比例函数的性质即可确定k的值.
查看更多完整答案,请扫码查看


