《2025年单元双测全优测评卷九年级数学下册人教版》

22. (8分)[情境创新类问题](2023·兰州中考)如图(1)是我国第一个以“龙”为主题的主题公园——“兰州龙源”，“兰州龙源”的“龙”字主题雕塑以紫铜铸造，如巨龙腾空，气势如虹，屹立在黄河北岸，某数学兴趣小组开展了测量“龙”字雕塑CD高度的实践活动，具体过程如下，如图(2)，“龙”字雕塑CD位于垂直地面的基座BC上，在平行于水平地面的A处测得∠BAC = 38°，∠BAD = 53°，AB = 18 m. 求“龙”字雕塑CD的高度.(B，C，D三点共线，BD⊥AB，结果精确到0.1 m. 参考数据：sin 38°≈0.62，cos 38°≈0.79，tan 38°≈0.78，sin 53°≈0.80，cos 53°≈0.60，tan 53°≈1.33)

答案： 在$Rt\triangle ABC$中，$AB = 18$ m，$\angle BAC = 38^{\circ}$，
$\because\tan\angle BAC=\frac{BC}{AB}$，
$\therefore BC = AB\cdot\tan\angle BAC = 18\times\tan38^{\circ}\approx18\times0.78 = 14.04$(m).
在$Rt\triangle ABD$中，$AB = 18$ m，$\angle BAD = 53^{\circ}$，
$\because\tan\angle BAD=\frac{BD}{AB}$，
$\therefore BD = AB\cdot\tan\angle BAD = 18\times\tan53^{\circ}\approx18\times1.33 = 23.94$(m)，
$\therefore CD = BD - BC\approx23.94 - 14.04 = 9.9$(m).
故“龙”字雕塑 CD 的高度约为 9.9 m.

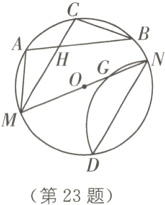
23. (8分)(2023·绥化中考)如图，MN为⊙O的直径，且MN = 15，MC与ND为圆内的一组平行弦，弦AB交MC于点H. 点A在$\overset{\frown}{MC}$上，点B在$\overset{\frown}{NC}$上，∠OND + ∠AHM = 90°.
(1)求证：MH·CH = AH·BH；
(2)求证：$\overset{\frown}{AC}=\overset{\frown}{BC}$；
(3)在⊙O中，沿弦ND所在的直线作劣弧$\overset{\frown}{ND}$的轴对称图形，使其交直径MN于点G. 若sin∠CMN = $\frac{3}{5}$，求NG的长.

答案：

(1)$\because\angle ABC$和$\angle AMC$都是$\overset{\frown}{AC}$所对的圆周角，
$\therefore\angle ABC=\angle AMC$.
$\because\angle AHM=\angle CHB$，$\therefore\triangle AMH\sim\triangle CBH$，
$\therefore\frac{AH}{CH}=\frac{MH}{BH}$，$\therefore MH\cdot CH = AH\cdot BH$.
(2)如图，连接 OC，交 AB 于点 F.
$\because MC$与 ND 为一组平行弦，即$MC// ND$，
$\therefore\angle OND=\angle OMC$.
$\because OM = OC$，$\therefore\angle OMC=\angle OCM$.
$\because\angle OND+\angle AHM = 90^{\circ}$，
$\therefore\angle OCM+\angle AHM=\angle OCM+\angle CHB = 90^{\circ}$，
$\therefore\angle HFC = 90^{\circ}$，$\therefore OC\perp AB$，$\therefore\overset{\frown}{AC}=\overset{\frown}{BC}$.

(3)如图，连接 DM，DG，过点 D 作$DE\perp MN$，垂足为 E，设点 G 的对称点为$G'$，连接$G'D$，$G'N$，$G'G$，
$\therefore DG = DG'$，$\angle G'ND=\angle GND$，$\therefore DG' = DM$，
$\therefore DG = DM$，
$\therefore\triangle DGM$是等腰三角形.
$\because DE\perp MN$，$\therefore GE = ME$.
$\because MN$为直径，$\therefore\angle MDN = 90^{\circ}$，
$\therefore\angle EDM+\angle EDN = 90^{\circ}$.
$\because DE\perp MN$，$\therefore\angle DEN = 90^{\circ}$，
$\therefore\angle DNM+\angle EDN = 90^{\circ}$，$\therefore\angle EDM=\angle DNM$.
又$\angle DNM=\angle CMN$，
$\therefore\sin\angle EDM=\sin\angle DNM=\sin\angle CMN=\frac{3}{5}$.
在$Rt\triangle MND$中，$MN = 15$，
$\therefore\sin\angle DNM=\frac{MD}{MN}=\frac{MD}{15}=\frac{3}{5}$，$\therefore MD = 9$.
在$Rt\triangle MED$中，$\sin\angle EDM=\frac{3}{5}=\frac{ME}{MD}$，
$\therefore\frac{ME}{9}=\frac{3}{5}$，$\therefore ME=\frac{27}{5}$，
$\therefore NG = MN - MG = MN - 2ME = 15 - 2\times\frac{27}{5}=\frac{21}{5}$.
故 NG 的长为$\frac{21}{5}$.