2025年单元双测全优测评卷九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
24.(10分)(2023·湖南永州祁阳期末)阅读下面材料:
小波遇到这样一个问题:如图(1),在△ABC中,BE是边AC上的中线,点D在边BC上,AD与BE相交于点P.
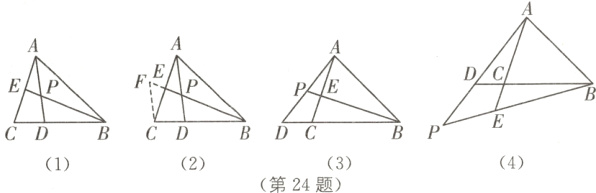
(1)小波发现,$\frac{DB}{BC}=\frac{2}{3}$,过点C作CF//AD,交BE的延长线于点F,通过构造△CEF(如图(2)),经过推理和计算得到$\frac{AP}{PD}$的值为_______.
(2)参考小波思考问题的方法,解决问题:
①如图(3),在△ABC中,点D在BC的延长线上,$\frac{DB}{BC}=\frac{4}{3}$,点E在AC上,且$\frac{AE}{EC}=\frac{3}{2}$,求$\frac{AP}{PD}$的值;
②如图(4),在△ABC中,点D在BC的延长线上,$\frac{DB}{BC}=\frac{4}{3}$,点E在AC的延长线上,且$\frac{AE}{EC}=\frac{7}{2}$,求出$\frac{AP}{PD}$的值.
小波遇到这样一个问题:如图(1),在△ABC中,BE是边AC上的中线,点D在边BC上,AD与BE相交于点P.

(1)小波发现,$\frac{DB}{BC}=\frac{2}{3}$,过点C作CF//AD,交BE的延长线于点F,通过构造△CEF(如图(2)),经过推理和计算得到$\frac{AP}{PD}$的值为_______.
(2)参考小波思考问题的方法,解决问题:
①如图(3),在△ABC中,点D在BC的延长线上,$\frac{DB}{BC}=\frac{4}{3}$,点E在AC上,且$\frac{AE}{EC}=\frac{3}{2}$,求$\frac{AP}{PD}$的值;
②如图(4),在△ABC中,点D在BC的延长线上,$\frac{DB}{BC}=\frac{4}{3}$,点E在AC的延长线上,且$\frac{AE}{EC}=\frac{7}{2}$,求出$\frac{AP}{PD}$的值.
答案:
(1)$\frac{3}{2}$ [解析]
∵PD//FC,
∴△BPD∽△BFC,
∴$\frac{PD}{FC}$=$\frac{BD}{BC}$=$\frac{2}{3}$.
∵BE是边AC上的中线,
∴AE = CE = $\frac{1}{2}$AC.
∵AP//CF,
∴△APE∽△CFE,
∴$\frac{AP}{CF}$=$\frac{AE}{CE}$ = 1,
∴$\frac{AP}{PD}$=$\frac{3}{2}$.
(2)①如图
(1),过点A作AF//BC,交BP的延长线于点F,
∴△AFE∽△CBE,
∴$\frac{AF}{BC}$=$\frac{AE}{EC}$=$\frac{3}{2}$.
设AF = 3x,BC = 2x.
∵$\frac{DB}{BC}$=$\frac{4}{3}$,
∴BD = $\frac{8}{3}$x.
∵AF//BD,
∴△AFP∽△DBP,
∴$\frac{AP}{PD}$=$\frac{AF}{BD}$=$\frac{9}{8}$. 故$\frac{AP}{PD}$的值为$\frac{9}{8}$;
②如图
(2),过点C作CF//AP交PB于点F,
∴△BCF∽△BDP,
∴$\frac{CF}{PD}$=$\frac{BC}{BD}$=$\frac{3}{4}$.
设CF = 3x,PD = 4x,
∵CF//AP,
∴△ECF∽△EAP,
∴$\frac{CF}{AP}$=$\frac{EC}{AE}$=$\frac{2}{7}$,
∴AP = $\frac{21}{2}$x,
∴$\frac{AP}{DP}$=$\frac{\frac{21}{2}x}{4x}$=$\frac{21}{8}$. 故$\frac{AP}{PD}$的值为$\frac{21}{8}$.


(1)$\frac{3}{2}$ [解析]
∵PD//FC,
∴△BPD∽△BFC,
∴$\frac{PD}{FC}$=$\frac{BD}{BC}$=$\frac{2}{3}$.
∵BE是边AC上的中线,
∴AE = CE = $\frac{1}{2}$AC.
∵AP//CF,
∴△APE∽△CFE,
∴$\frac{AP}{CF}$=$\frac{AE}{CE}$ = 1,
∴$\frac{AP}{PD}$=$\frac{3}{2}$.
(2)①如图
(1),过点A作AF//BC,交BP的延长线于点F,
∴△AFE∽△CBE,
∴$\frac{AF}{BC}$=$\frac{AE}{EC}$=$\frac{3}{2}$.
设AF = 3x,BC = 2x.
∵$\frac{DB}{BC}$=$\frac{4}{3}$,
∴BD = $\frac{8}{3}$x.
∵AF//BD,
∴△AFP∽△DBP,
∴$\frac{AP}{PD}$=$\frac{AF}{BD}$=$\frac{9}{8}$. 故$\frac{AP}{PD}$的值为$\frac{9}{8}$;
②如图
(2),过点C作CF//AP交PB于点F,
∴△BCF∽△BDP,
∴$\frac{CF}{PD}$=$\frac{BC}{BD}$=$\frac{3}{4}$.
设CF = 3x,PD = 4x,
∵CF//AP,
∴△ECF∽△EAP,
∴$\frac{CF}{AP}$=$\frac{EC}{AE}$=$\frac{2}{7}$,
∴AP = $\frac{21}{2}$x,
∴$\frac{AP}{DP}$=$\frac{\frac{21}{2}x}{4x}$=$\frac{21}{8}$. 故$\frac{AP}{PD}$的值为$\frac{21}{8}$.


查看更多完整答案,请扫码查看


