《2025年单元双测全优测评卷九年级数学下册人教版》

15. 如图，在Rt△ABC中，∠ABC = 90°，∠ACB = 30°，将△ABC绕点A按逆时针方向旋转15°后得到△AB₁C₁，B₁C₁交AC于点D，如果AD = 2$\sqrt{2}$，那么△ABC的周长为________.

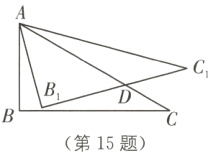
答案： $6 + 2\sqrt{3}$

16. (2023·武汉中考)如图，将45°的∠AOB按下面的方式放置在一把刻度尺上：顶点O与尺下沿的端点重合，OA与尺下沿重合，OB与尺上沿的交点B在尺上的读数为2 cm，若按相同的方式将37°的∠AOC放置在该刻度尺上，则OC与尺上沿的交点C在尺上的读数是________cm(结果精确到0.1 cm，参考数据sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75).

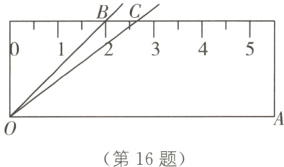
答案：
2.7 cm ［解析］如图，过点 B 作$BD\perp OA$于 D，过点 C 作$CE\perp OA$于 E.
在$\triangle BOD$中，$\angle BDO = 90^{\circ}$，$\angle DOB = 45^{\circ}$，
$\therefore CE = BD = 2$ cm.
在$\triangle OCE$中，$\angle COE = 37^{\circ}$，$\angle CEO = 90^{\circ}$，
$\therefore\tan37^{\circ}=\frac{CE}{OE}\approx0.75$，$\therefore OE\approx2.7$ cm，
即 OC 与尺上沿的交点 C 在尺上的读数是 2.7 cm.

17. (2023·赤峰中考)为发展城乡经济，建设美丽乡村，某乡对A地和B地之间的一处垃圾填埋场进行改造，把原来A地去往B地需要绕行到C地的路线，改造成可以直线通行的公路AB. 如图，经勘测，AC = 6千米，∠CAB = 60°，∠CBA = 37°，则改造后公路AB的长是________千米.(精确到0.1千米. 参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75，$\sqrt{3}\approx1.73$)

答案：
9.9 ［解析］如图，过点 C 作$CD\perp AB$，垂足为 D，
在$Rt\triangle ADC$中，$AC = 6$千米，$\angle CAB = 60^{\circ}$，
$\cos\angle CAB=\frac{AD}{AC}$，$\sin\angle CAB=\frac{CD}{AC}$，
$\therefore AD = AC\times\cos\angle CAB = 6\times\cos60^{\circ}=3$(千米)，
$CD = AC\sin\angle CAB = 6\times\sin60^{\circ}=3\sqrt{3}$(千米).
在$Rt\triangle CDB$中，$\angle CBA = 37^{\circ}$，$CD = 3\sqrt{3}$千米，
$\tan\angle CBA=\frac{CD}{DB}$，
$\therefore DB=\frac{CD}{\tan\angle CBA}=\frac{3\sqrt{3}}{\tan37^{\circ}}\approx\frac{3\sqrt{3}}{0.75}=4\sqrt{3}$(千米)，
$\therefore AB = AD + DB = 3 + 4\sqrt{3}\approx9.9$(千米).
故改造后公路 AB 的长是 9.9 千米.

18. (2022·黄冈中考)如图，有甲乙两座建筑物，从甲建筑物A点处测得乙建筑物D点的俯角α为45°，C点的俯角β为58°，BC为两座建筑物的水平距离. 已知乙建筑物的高度CD为6 m，则甲建筑物的高度AB为________m.(sin 58°≈0.85，cos 58°≈0.53，tan 58°≈1.60，结果保留整数)

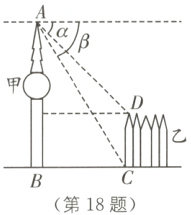
答案：
16 ［解析］如图，过 D 点作$DE\perp AB$于点 E，设$AE = x$ m，根据题意，得$AB\perp BC$，$DC\perp BC$，
$\therefore\angle AED=\angle BED=\angle ABC=\angle DCB = 90^{\circ}$.
$\therefore$四边形 BCDE 是矩形.
$\because$从甲建筑物 A 点处测得乙建筑物 D 点的俯角$\alpha$为$45^{\circ}$，C 点的俯角$\beta$为$58^{\circ}$，BC 为两座建筑物的水平距离，乙建筑物的高度 CD 为 6 m，
$\therefore BE = CD = 6$ m，$\angle ADE = 45^{\circ}$，$\angle ACB = 58^{\circ}$.
在$Rt\triangle ADE$中，$\angle ADE = 45^{\circ}$，
$\therefore\angle EAD = 90^{\circ}-\angle ADE = 45^{\circ}$.
$\therefore\angle EAD=\angle ADE$.$\therefore DE = AE = x$ m.
$\therefore BC = DE = x$ m.
$\therefore AB = AE + BE=(x + 6)$m.
在$Rt\triangle ABC$中，$\tan\angle ACB=\frac{AB}{BC}$，
即$\tan58^{\circ}=\frac{x + 6}{x}\approx1.60$，解得$x\approx10$.
经检验，$x\approx10$是原分式方程的解且符合题意.$\therefore AB = x + 6\approx16$ m.

19. (6分)计算：
(1)$\sqrt{3}\cos 30^{\circ}+\sqrt{2}\sin 45^{\circ}$； (2)-2²+$\sqrt{8}\sin 45^{\circ}-2^{-1}+(\sqrt{2}-1)^{0}$.

答案：
(1)原式$=\sqrt{3}\times\frac{\sqrt{3}}{2}+\sqrt{2}\times\frac{\sqrt{2}}{2}=\frac{5}{2}$.
(2)原式$=-4 + 2\sqrt{2}\times\frac{\sqrt{2}}{2}-\frac{1}{2}+1$
$=-4 + 2-\frac{1}{2}+1=-\frac{3}{2}$.