《2025年单元双测全优测评卷九年级数学下册人教版》

7. [情境创新类问题]（2023·苏州中考）今天是父亲节，小东同学准备送给父亲一个小礼物. 已知礼物外包装的主视图如图所示，则该礼物的外包装不可能是（ ）.

A. 长方体
B. 正方体
C. 圆柱
D. 三棱锥

答案： D

8. （2022·贵港中考）如图，某数学兴趣小组测量一棵树$CD$的高度，在点$A$处测得树顶$C$的仰角为$45^{\circ}$，在点$B$处测得树顶$C$的仰角为$60^{\circ}$，且$A$，$B$，$D$三点在同一直线上，若$AB = 16\ m$，则这棵树$CD$的高度是（ ）.

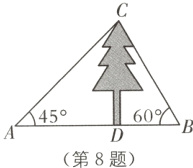
A. $8(3 - \sqrt{3})\ m$
B. $8(3 + \sqrt{3})\ m$
C. $6(3 - \sqrt{3})\ m$
D. $6(3 + \sqrt{3})\ m$

答案： A [解析]设$CD = x$，在$Rt\triangle ADC$中，$\angle A = 45^{\circ}$，
$\therefore CD = AD = x$，$\therefore BD = 16 - x$。
在$Rt\triangle BCD$中，$\angle B = 60^{\circ}$，$\therefore\tan B=\frac{CD}{BD}$，
即$\frac{x}{16 - x}=\sqrt{3}$，解得$x = 8(3-\sqrt{3})$。故选 A。

9. 如图，已知第一象限内的点$A$在反比例函数$y = \frac{2}{x}$的图象上，第二象限内的点$B$在反比例函数$y = \frac{k}{x}$的图象上，且$OA\perp OB$，$\cos A = \frac{\sqrt{3}}{3}$，则$k$的值为（ ）.

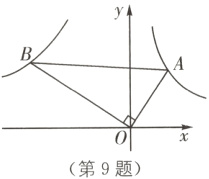
A. -3
B. -4
C. $-\sqrt{3}$
D. $-2\sqrt{3}$

答案：
B [解析]如图，过点 A 作$AE\perp x$轴，过点 B 作$BF\perp x$轴，
$\because OA\perp OB$，
$\therefore\angle AOB = 90^{\circ}$。
$\therefore\angle BOF+\angle EOA = 90^{\circ}$。

$\because\angle BOF+\angle FBO = 90^{\circ}$，
$\therefore\angle EOA=\angle FBO$。
$\because\angle BFO=\angle OEA = 90^{\circ}$，
$\therefore\triangle BFO\sim\triangle OEA$。
$\because$在$Rt\triangle AOB$中，$\cos\angle BAO=\frac{AO}{AB}=\frac{\sqrt{3}}{3}$，
$\therefore$设$AB=\sqrt{3}a$，则$OA = a$，根据勾股定理得$BO=\sqrt{2}a$，$\therefore OB:OA=\sqrt{2}:1$。
$\therefore S_{\triangle BFO}:S_{\triangle OEA}=2:1$。
$\because$点 A 在反比例函数$y=\frac{2}{x}$上，
$\therefore S_{\triangle OEA}=1$，$\therefore S_{\triangle BFO}=2$，则$k = - 4$。

10. 如图，$AB$是$\odot O$的直径，弦$CD\perp AB$于点$G$，点$F$是$CD$上一点，且满足$\frac{CF}{FD} = \frac{1}{3}$，连接$AF$并延长交$\odot O$于点$E$，连接$AD$，$DE$，若$CF = 2$，$AF = 3$，给出下列结论：①$\triangle ADF\sim\triangle AED$；②$FG = 2$；③$\tan E = \frac{\sqrt{5}}{2}$；④$S_{\triangle DEF} = 4\sqrt{5}$. 其中正确的是（ ）.

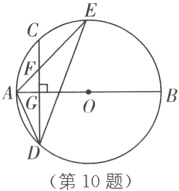
A. ①②③
B. ②③④
C. ①②④
D. ①③④

答案： C [解析]①$\because AB$是$\odot O$的直径，弦$CD\perp AB$，
$\therefore\overset{\frown}{AD}=\overset{\frown}{AC}$，$DG = CG$，$\therefore\angle ADF=\angle AED$。
$\because\angle FAD=\angle DAE$(公共角)，$\therefore\triangle ADF\sim\triangle AED$，
故①正确；②$\because\frac{CF}{FD}=\frac{1}{3}$，$CF = 2$，$\therefore FD = 6$，$\therefore CD = DF + CF = 8$，$\therefore CG = DG = 4$，$\therefore FG = CG - CF = 2$，故②正确；③$\because AF = 3$，$FG = 2$，$\therefore AG=\sqrt{AF^{2}-FG^{2}}=\sqrt{3^{2}-2^{2}}=\sqrt{5}$，$\therefore$在$Rt\triangle AGD$中，$\tan\angle ADG=\frac{AG}{DG}=\frac{\sqrt{5}}{4}$，$\therefore\tan E=\frac{\sqrt{5}}{4}$，故③错误；④$\because DF = DG + FG = 6$，$AD=\sqrt{AG^{2}+DG^{2}}=\sqrt{5 + 4^{2}}=\sqrt{21}$，$\therefore S_{\triangle ADF}=\frac{1}{2}DF\cdot AG=\frac{1}{2}\times6\times\sqrt{5}=3\sqrt{5}$。
$\because\triangle ADF\sim AED$，$\therefore\frac{S_{\triangle ADF}}{S_{\triangle AED}}=(\frac{AF}{AD})^{2}=(\frac{3}{\sqrt{21}})^{2}=\frac{3}{7}$，$\therefore S_{\triangle AED}=7\sqrt{5}$，$\therefore S_{\triangle DEF}=S_{\triangle AED}-S_{\triangle ADF}=4\sqrt{5}$，故④正确，故选 C。

11. 在直角三角形$ABC$中，$\sin A$的值为$\frac{1}{2}$，则$\cos A$的值为____.

答案： $\frac{\sqrt{3}}{2}$

12. 将如图所示的图形剪去一个小正方形，使余下的部分恰好能折成一个正方体，下列序号为1，2，3，6的小正方形不能剪去的是________.（填序号）

答案： 3