《2025年单元双测全优测评卷九年级数学下册人教版》

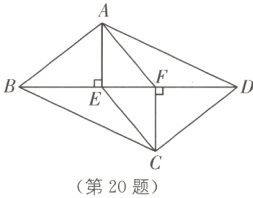
20. (6分)如图，在□ABCD中，E，F是对角线BD上的两点(点E在点F左侧)，且∠AEB = ∠CFD = 90°.
(1)求证：四边形AECF是平行四边形；
(2)当AB = 5，tan∠ABE = $\frac{3}{4}$，∠CBE = ∠EAF时，求BD的长.

答案：
(1)$\because\angle AEB=\angle CFD = 90^{\circ}$，
$\therefore AE\perp BD$，$CF\perp BD$，$\therefore AE// CF$.
$\because$四边形 ABCD 是平行四边形，
$\therefore AB = CD$，$AB// CD$.$\therefore\angle ABE=\angle CDF$.
在$\triangle ABE$和$\triangle CDF$中，$\begin{cases}\angle AEB=\angle CFD,\\\angle ABE=\angle CDF,\\AB = CD,\end{cases}$
$\therefore\triangle ABE\cong\triangle CDF$(AAS)，$\therefore AE = CF$.
$\therefore$四边形 AECF 是平行四边形.
(2)在$Rt\triangle ABE$中，$\tan\angle ABE=\frac{3}{4}=\frac{AE}{BE}$，设$AE = 3a$，则$BE = 4a$，
由勾股定理，得$(3a)^{2}+(4a)^{2}=5^{2}$，
解得$a = 1$或$a = -1$(舍去).
$\therefore AE = 3$，$BE = 4$.
由
(1)得，四边形 AECF 是平行四边形，
$\therefore\angle EAF=\angle ECF$，$CF = AE = 3$.
$\because\angle CBE=\angle EAF$，$\therefore\angle ECF=\angle CBE$.
$\therefore\tan\angle CBE=\tan\angle ECF$.
$\therefore\frac{CF}{BF}=\frac{EF}{CF}$.$\therefore CF^{2}=EF\cdot BF$.
设$EF = x$，则$BF = x + 4$，$\therefore3^{2}=x(x + 4)$，
解得$x=\sqrt{13}-2$或$x=-\sqrt{13}-2$(舍去)，即$EF=\sqrt{13}-2$.
由
(1)，得$\triangle ABE\cong\triangle CDF$，
$\therefore BE = DF = 4$.$\therefore BD = BE + EF + DF = 4+\sqrt{13}-2 + 4 = 6+\sqrt{13}$.

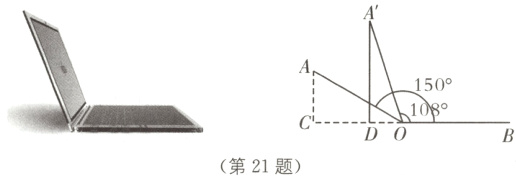
21. (8分)(2022·成都中考)2022年6月6日是第27个全国“爱眼日”，某数学兴趣小组开展了“笔记本电脑的张角大小、顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动. 如图，当张角∠AOB = 150°时，顶部边缘A处离桌面的高度AC的长为10 cm，此时用眼舒适度不太理想. 小组成员调整张角大小继续探究，最后联系黄金比知识，发现当张角∠A'OB = 108°时(点A'是A的对应点)，用眼舒适度较为理想. 求此时顶部边缘A'处离桌面的高度A'D的长.(结果精确到1 cm，参考数据：sin 72°≈0.95，cos 72°≈0.31，tan 72°≈3.08)

答案： 在$Rt\triangle ACO$中，$\angle AOC = 180^{\circ}-\angle AOB = 30^{\circ}$，$AC = 10$ cm，
$\therefore OA=\frac{AC}{\sin30^{\circ}}=\frac{10}{\frac{1}{2}}=20$.
在$Rt\triangle A'DO$中，$\angle A'OC = 180^{\circ}-\angle A'OB = 72^{\circ}$，$OA' = OA = 20$ cm，
$\therefore A'D = OA'\cdot\sin72^{\circ}\approx20\times0.95 = 19$ cm.