《2025年单元双测全优测评卷九年级数学下册人教版》

1.(2022·天津中考)tan 45°的值等于( ).
A. 2
B. 1
C. $\frac{\sqrt{2}}{2}$
D. $\frac{\sqrt{3}}{3}$

答案： B

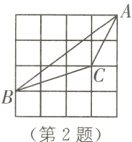
2.(2022·贵港中考)如图，在4×4网格正方形中，每个小正方形的边长为1，顶点为格点，若△ABC的顶点均是格点，则cos∠BAC的值是( ).

A. $\frac{\sqrt{5}}{5}$
B. $\frac{\sqrt{10}}{5}$
C. $\frac{2\sqrt{5}}{5}$
D. $\frac{4}{5}$

答案：
C [解析]过点C作AB的垂线交AB于点D，如图所示，

∵每个小正方形的边长为1，
∴AC = $\sqrt{5}$，BC = $\sqrt{10}$，AB = 5.
设AD = x，则BD = 5 - x，
在Rt△ACD中，DC² = AC² - AD²，
在Rt△BCD中，DC² = BC² - BD²，
∴10 - (5 - x)² = 5 - x²，解得x = 2.
∴cos∠BAC = $\frac{AD}{AC}$ = $\frac{2}{\sqrt{5}}$ = $\frac{2\sqrt{5}}{5}$. 故选C.

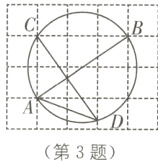
3.(2022·通辽中考)如图，由边长为1的小正方形构成的网格中，点A，B，C都在格点上，以AB为直径的圆经过点C，D，则cos∠ADC的值为( ).

A. $\frac{2\sqrt{13}}{13}$
B. $\frac{3\sqrt{13}}{13}$
C. $\frac{2}{3}$
D. $\frac{\sqrt{5}}{3}$

答案： B [解析]连接AC，AB，
∵AB为圆的直径，
∴∠ACB = 90°.
又点A，B，C都在格点上，
∴∠ADC = ∠ABC.
在Rt△ABC中，cos∠ABC = $\frac{BC}{AB}$ = $\frac{3}{\sqrt{3^{2}+2^{2}}}$ = $\frac{3\sqrt{13}}{13}$ = cos∠ADC. 故选B.
方法诠释：根据圆周角定理将所求角转化到直角三角形中，再求其余弦值.

4. 已知α为锐角，且sin α=$\frac{1}{2}$，则α的值是( ).
A. 30°
B. 45°
C. 60°
D. 75°

答案： A

5. 在Rt△ABC中，若∠C=90°，AC=2，AB=3，则cos B的值为( ).
A. $\frac{2}{3}$
B. $\frac{\sqrt{5}}{3}$
C. $\frac{3}{2}$
D. $\frac{\sqrt{5}}{2}$

答案： B

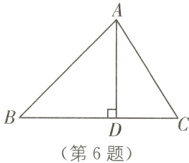
6.(2022·陕西中考)如图，AD是△ABC的高，若BD=2CD=6，tan C=2，则边AB的长为( ).

A. 3$\sqrt{2}$
B. 3$\sqrt{5}$
C. 3$\sqrt{7}$
D. 6$\sqrt{2}$

答案： D [解析]
∵BD = 2CD = 6，
∴CD = 3.
∵在Rt△ADC中，tan C = 2，
∴AD = CD·tan C = 3×2 = 6.
在Rt△ABD中，由勾股定理，得AB = $\sqrt{AD^{2}+BD^{2}}$ = $\sqrt{6^{2}+6^{2}}$ = 6$\sqrt{2}$. 故选D.

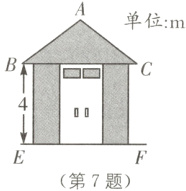
7.(2022·金华中考)一配电房示意图如图所示，它是一个轴对称图形，已知BC=6 m，∠ABC=α，则房顶A离地面EF的高度为( ).

A. (4＋3sin α)m
B. (4＋3tan α)m
C. $(4+\frac{3}{\sin\alpha})$m
D. $(4+\frac{3}{\tan\alpha})$m

答案：
B [解析]过点A作AD⊥BC于点D，如图所示.

∵它是一个轴对称图形，
∴BD = DC = $\frac{1}{2}$BC = 3 m.
∴tanα = $\frac{AD}{BD}$ = $\frac{AD}{3}$，
即AD = 3tanα.
∴房顶A离地面EF的高度为(4 + 3tanα)m. 故选B.