《2025年单元双测全优测评卷九年级数学下册人教版》

6.(2022·舟山中考)如图，在Rt△ABC和Rt△BDE中，∠ABC = ∠BDE = 90°，点A在边DE的中点上，若AB = BC，DB = DE = 2，连接CE，则CE的长为( ).

A. $\sqrt{14}$
B. $\sqrt{15}$
C. 4
D. $\sqrt{17}$

答案： D [解析]如图,过点E作EF⊥BC,交CB延长线于点F,过点A作AG⊥BE于点G,
在Rt△BDE中,∠BDE=90°,DB=DE=2,
∴BE=$\sqrt{BD^{2}+DE^{2}}$=2$\sqrt{2}$,∠BED=45°.
∵点A在边DE的中点上,
∴AD=AE=1,
∴AB=$\sqrt{AD^{2}+BD^{2}}$=$\sqrt{5}$,
∴AB=BC=$\sqrt{5}$.
∵∠BED=45°,
∴△AEG是等腰直角三角形,
∴EG=AG=$\frac{\sqrt{2}}{2}$AE=$\frac{\sqrt{2}}{2}$,
∴BG=$\frac{3\sqrt{2}}{2}$.
∵∠ABC=∠F=90°,
∴EF//AB,
∴∠BEF=∠ABG,
∴△BEF∽△ABG,
∴$\frac{BE}{AB}=\frac{BF}{AG}=\frac{EF}{BG}$,即$\frac{2\sqrt{2}}{\sqrt{5}}=\frac{BF}{\frac{\sqrt{2}}{2}}=\frac{EF}{\frac{3\sqrt{2}}{2}}$,
解得BF=$\frac{2\sqrt{5}}{5}$,EF=$\frac{6\sqrt{5}}{5}$,
∴CF=$\frac{7\sqrt{5}}{5}$,
∴CE=$\sqrt{EF^{2}+CF^{2}}$=$\sqrt{17}$. 故选D.

7.如图是某几何体的三视图，根据图中数据，求得该几何体的体积为( ).

A. 60π
B. 70π
C. 90π
D. 160π

答案： B

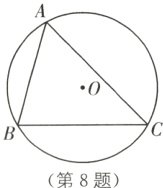
8.(2022·杭州中考)如图，已知△ABC内接于半径为1的⊙O，∠BAC = θ(θ是锐角)，则△ABC的面积的最大值为( ).
A. cosθ(1 + cosθ) B. cosθ(1 + sinθ)
C. sinθ(1 + sinθ) D. sinθ(1 + cosθ)
　

答案： D [解析]当△ABC的高AD经过圆的圆心时,此时△ABC的面积最大,如图所示.
∵A'D⊥BC,
∴BC=2BD,
∠BOD=∠BAC=θ,
在Rt△BOD中,
sinθ=$\frac{BD}{OB}=\frac{BD}{1}$,
cosθ=$\frac{OD}{OB}=\frac{OD}{1}$,
∴BD=sinθ,OD=cosθ,
∴BC=2BD=2sinθ,
A'D=A'O+OD=1+cosθ,
∴S△ABC=$\frac{1}{2}$A'D·BC=$\frac{1}{2}$·2sinθ(1+cosθ)=sinθ(1+cosθ). 故选D.

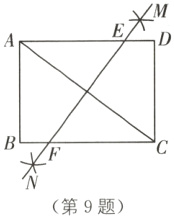
9.(2022·辽宁中考)如图，在矩形ABCD中，AB = 6，BC = 8，分别以点A和点C为圆心，以大于$\frac{1}{2}$AC的长为半径作弧，两弧相交于点M和点N，作直线MN分别交AD，BC于点E，F，则AE的长为( ).
A. $\frac{7}{4}$ B. $\frac{9}{4}$ C. $\frac{15}{4}$ D. $\frac{25}{4}$
　　

答案： D [解析]设MN与AC的交点为O,
∵四边形ABCD为矩形,
∴∠ADC=90°,AB=DC=6,BC=AD=8,
∴△ADC为直角三角形.
∵CD=6,AD=8,
∴AC=$\sqrt{AD^{2}+DC^{2}}$=$\sqrt{8^{2}+6^{2}}$=10,
cos∠CAD=$\frac{AD}{AC}=\frac{8}{10}=\frac{4}{5}$.
又由作图知MN为AC的垂直平分线,
∴∠MOA=90°,AO=$\frac{1}{2}$AC=5,
∴在Rt△AOE中,cos∠EAO=$\frac{AO}{AE}$.
∵cos∠CAD=cos∠EAO,
∴$\frac{5}{AE}=\frac{4}{5}$,
∴AE=$\frac{25}{4}$. 故选D.

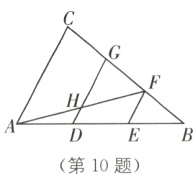
10.(2023·内江中考)如图，在△ABC中，点D，E为边AB的三等分点，点F，G在边BC上，AC//DG//EF，点H为AF与DG的交点.若AC = 12，则DH的长为( ).
A. 1 B. $\frac{3}{2}$ C. 2 D. 3
　　

答案： C [解析]
∵点D,E为边AB的三等分点,
∴AD=DE=EB,
∴AB=3BE,AE=2AD.
∵EF//AC,
∴△BEF∽△BAC,
∴EF∶AC=BE∶AB.
∵AC=12,AB=3BE,
∴EF∶12=BE∶3BE,
∴EF=4.
∵DG//EF,
∴△ADH∽△AEF,
∴DH∶EF=AD∶AE.
∵EF=4,AE=2AD,
∴DH∶4=AD∶2AD,
∴DH=2. 故选C.