《2025年单元双测全优测评卷九年级数学下册人教版》

22. （12分）如图，$AB$是$\odot O$的直径，点$E$为$\odot O$上一点，点$D$是$\overset{\frown}{AE}$上一点，连接$AE$并延长至点$C$，使$\angle CBE = \angle BDE$，$BD$与$AE$交于点$F$.
（1）求证：$BC$是$\odot O$的切线；
（2）若$BD$平分$\angle ABE$，求证：$AD^2 = DF\cdot BD$.

答案：
(1)$\because AB$是$\odot O$的直径，$\therefore\angle AEB = 90^{\circ}$，
$\therefore\angle EAB+\angle EBA = 90^{\circ}$。
$\because\angle CBE=\angle BDE$，$\angle BDE=\angle EAB$，
$\therefore\angle EAB=\angle CBE$，$\therefore\angle EBA+\angle CBE = 90^{\circ}$，
即$\angle ABC = 90^{\circ}$，$\therefore CB\perp AB$。
$\because AB$是$\odot O$的直径，$\therefore BC$是$\odot O$的切线。
(2)$\because BD$平分$\angle ABE$，$\therefore\angle ABD=\angle DBE$。
$\because\angle DAF=\angle DBE$，$\therefore\angle DAF=\angle ABD$。
$\because\angle ADB=\angle ADF$，$\therefore\triangle ADF\sim\triangle BDA$，
$\therefore\frac{AD}{BD}=\frac{DF}{AD}$，$\therefore AD^{2}=DF\cdot BD$。

23. （14分）为了测量如图所示的两岸平行的河流宽度，三个数学研究小组设计了不同的方案，他们在河南岸的点$A$处测得河北岸的树$H$恰好在$A$的正北方向. 测量方案与数据如表：

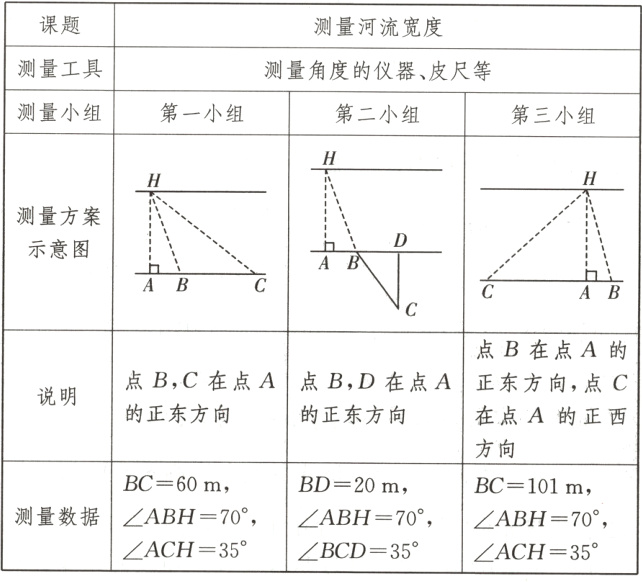
（1）哪个小组的数据无法计算出河宽？
（2）请选择其中一个方案及其数据求出河宽（精确到$0.1\ m$，参考数据：$\sin 70^{\circ} \approx 0.94$，$\sin 35^{\circ} \approx 0.57$，$\tan 70^{\circ} \approx 2.75$，$\tan 35^{\circ} \approx 0.70$）.

答案：
(1)第二小组的数据无法计算出河宽。
(2)第一小组的解法：$\because\angle ABH=\angle ACH+\angle BHC$，$\angle ABH = 70^{\circ}$，$\angle ACH = 35^{\circ}$，
$\therefore\angle BHC=\angle BCH = 35^{\circ}$，$\therefore BC = BH = 60$m，
$\therefore AH = BH\cdot\sin70^{\circ}\approx60\times0.94\approx56.4$(m)。
故河宽约为 56.4 m。
第三小组的解法：设$AH = x$m，则$CA=\frac{AH}{\tan35^{\circ}}$，$AB=\frac{AH}{\tan70^{\circ}}$。$\because CA + AB = CB$，
$\therefore\frac{x}{0.70}+\frac{x}{2.75}\approx101$，解得$x\approx56.4$。
故河宽约为 56.4 m。