2025年单元双测全优测评卷九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 已知β为锐角,cos β≤$\frac{1}{2}$,则β的取值范围为( ).
A. $30^{\circ}\leq\beta<90^{\circ}$
B. $0^{\circ}<\beta\leq60^{\circ}$
C. $60^{\circ}\leq\beta<90^{\circ}$
D. $30^{\circ}\leq\beta<60^{\circ}$
A. $30^{\circ}\leq\beta<90^{\circ}$
B. $0^{\circ}<\beta\leq60^{\circ}$
C. $60^{\circ}\leq\beta<90^{\circ}$
D. $30^{\circ}\leq\beta<60^{\circ}$
答案:
C
2. 若tan α = 2,则$\frac{3\sin\alpha - \cos\alpha}{4\sin\alpha + 2\cos\alpha}$的值为( ).
A. $\frac{1}{3}$
B. $\frac{5}{6}$
C. $\frac{1}{2}$
D. 1
A. $\frac{1}{3}$
B. $\frac{5}{6}$
C. $\frac{1}{2}$
D. 1
答案:
C [解析]因为$\tan\alpha=\frac{\sin\alpha}{\cos\alpha}=2$,
∴ 原式 =$\frac{\frac{3\sin\alpha}{\cos\alpha}-1}{\frac{4\sin\alpha}{\cos\alpha}+2}=\frac{3\tan\alpha - 1}{4\tan\alpha + 2}=\frac{3\times2 - 1}{4\times2 + 2}=\frac{1}{2}$.
故选 C.
∴ 原式 =$\frac{\frac{3\sin\alpha}{\cos\alpha}-1}{\frac{4\sin\alpha}{\cos\alpha}+2}=\frac{3\tan\alpha - 1}{4\tan\alpha + 2}=\frac{3\times2 - 1}{4\times2 + 2}=\frac{1}{2}$.
故选 C.
3. 若α为锐角,且tan α > $\sqrt{3}$,则α的取值范围是( ).
A. $60^{\circ}<\alpha<90^{\circ}$
B. $30^{\circ}<\alpha<60^{\circ}$
C. $45^{\circ}<\alpha<60^{\circ}$
D. $30^{\circ}>\alpha$
A. $60^{\circ}<\alpha<90^{\circ}$
B. $30^{\circ}<\alpha<60^{\circ}$
C. $45^{\circ}<\alpha<60^{\circ}$
D. $30^{\circ}>\alpha$
答案:
A
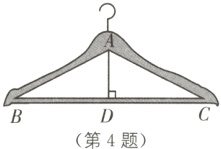
4. (2022·福建中考)如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB = AC,∠ABC = 27°,BC = 44 cm,则高AD约为( ).(参考数据:sin 27°≈0.45,cos 27°≈0.89,tan 27°≈0.51)
A. 9.90 cm
B. 11.22 cm
C. 19.58 cm
D. 22.44 cm

A. 9.90 cm
B. 11.22 cm
C. 19.58 cm
D. 22.44 cm
答案:
B
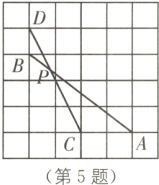
5. (2022·广元中考)如图,在正方形方格纸中,每个小正方形的边长都相等,A,B,C,D都在格点处,AB与CD相交于点P,则cos∠APC的值为( ).
A. $\frac{\sqrt{3}}{5}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{2}{5}$
D. $\frac{\sqrt{5}}{5}$

A. $\frac{\sqrt{3}}{5}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{2}{5}$
D. $\frac{\sqrt{5}}{5}$
答案:
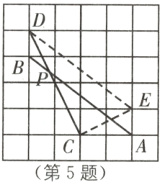
B [解析]把 AB 向上平移一个单位到 DE,连接CE,如图.
则$DE// AB$.
$\therefore\angle APC=\angle EDC$.
在$\triangle DCE$中,有$EC=\sqrt{2^{2}+1^{2}}=\sqrt{5}$,$DC=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$,$DE=\sqrt{3^{2}+4^{2}}=5$,
$\therefore EC^{2}+DC^{2}=5 + 20 = 25 = DE^{2}$.
$\therefore\triangle DCE$是直角三角形,且$\angle DCE = 90^{\circ}$.
$\therefore\cos\angle APC=\cos\angle EDC=\frac{DC}{DE}=\frac{2\sqrt{5}}{5}$.
故选 B.
B [解析]把 AB 向上平移一个单位到 DE,连接CE,如图.
则$DE// AB$.
$\therefore\angle APC=\angle EDC$.
在$\triangle DCE$中,有$EC=\sqrt{2^{2}+1^{2}}=\sqrt{5}$,$DC=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$,$DE=\sqrt{3^{2}+4^{2}}=5$,
$\therefore EC^{2}+DC^{2}=5 + 20 = 25 = DE^{2}$.
$\therefore\triangle DCE$是直角三角形,且$\angle DCE = 90^{\circ}$.
$\therefore\cos\angle APC=\cos\angle EDC=\frac{DC}{DE}=\frac{2\sqrt{5}}{5}$.

故选 B.
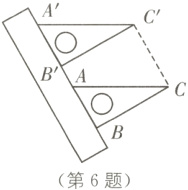
6. (2022·福建中考)如图,现有一把直尺和一块三角尺,其中∠ABC = 90°,∠CAB = 60°,AB = 8,点A对应直尺的刻度为12. 将该三角尺沿着直尺边缘平移,使得△ABC移动到△A'B'C',点A'对应直尺的刻度为0,则四边形ACC'A'的面积是( ).
A. 96
B. 96$\sqrt{3}$
C. 192
D. 160$\sqrt{3}$

A. 96
B. 96$\sqrt{3}$
C. 192
D. 160$\sqrt{3}$
答案:
B
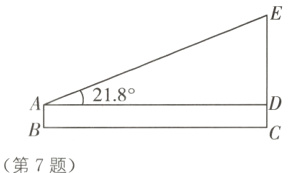
7. [情境创新类问题](2023·岳阳中考改编)2023年岳阳举办以“跃马江湖”为主题的马拉松赛事. 如图,某校数学兴趣小组在A处用仪器测得赛场一宣传气球顶部E处的仰角为21.8°,仪器与气球的水平距离BC为20米,且距地面高度AB为1.5米,则气球顶部离地面的高度EC是( )米(结果精确到0.1米,sin 21.8°≈0.3714,cos 21.8°≈0.9285,tan 21.8°≈0.4000).

A. 8
B. 9
C. 9.5
D. 10


A. 8
B. 9
C. 9.5
D. 10
答案:
C [解析]由题意,得四边形 ABCD 是矩形,
$\therefore AB = CD = 1.5$ m,$AD = BC = 20$ m,
在$Rt\triangle ADE$中,
$\because AD = BC = 20$ m,$\angle EAD = 21.8^{\circ}$,
$\therefore DE = AD\cdot\tan21.8^{\circ}\approx20\times0.4000 = 8$(m),
$\therefore CE = CD + DE = 1.5 + 8 = 9.5$(m),
故气球顶部离地面的高度 EC 是 9.5 m.
方法技巧本题考查了直角三角形的应用−仰角俯角问题,一般通过添加水平线、铅垂直线构造直角三角形,运用勾股定理、三角函数解答.
$\therefore AB = CD = 1.5$ m,$AD = BC = 20$ m,
在$Rt\triangle ADE$中,
$\because AD = BC = 20$ m,$\angle EAD = 21.8^{\circ}$,
$\therefore DE = AD\cdot\tan21.8^{\circ}\approx20\times0.4000 = 8$(m),
$\therefore CE = CD + DE = 1.5 + 8 = 9.5$(m),
故气球顶部离地面的高度 EC 是 9.5 m.
方法技巧本题考查了直角三角形的应用−仰角俯角问题,一般通过添加水平线、铅垂直线构造直角三角形,运用勾股定理、三角函数解答.
查看更多完整答案,请扫码查看


