2025年单元双测全优测评卷九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
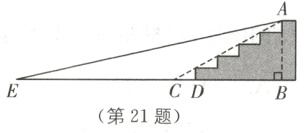
21.(10分)(2022·烟台中考)如图,某超市计划将门前的部分楼梯改造成无障碍通道.已知楼梯共有五级均匀分布的台阶,高AB = 0.75 m,斜坡AC的坡比为1:2,将要铺设的通道前方有一井盖,井盖边缘离楼梯底部的最短距离ED = 2.55 m.为防止通道遮盖井盖,所铺设通道的坡角不得小于多少度?(结果精确到1)
参考数据表
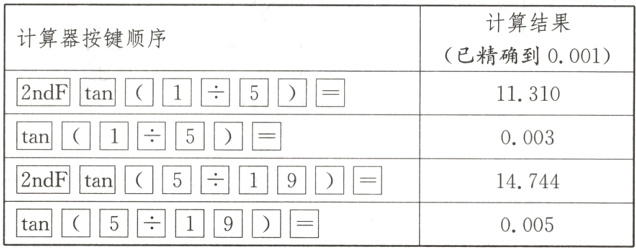
参考数据表


答案:
如图,
由题意,得DF=$\frac{1}{5}$AB=0.15 m,
∵斜坡AC的坡比为1∶2,
∴$\frac{AB}{BC}=\frac{1}{2}$,$\frac{DF}{CD}=\frac{1}{2}$,
∴BC=2AB=1.5 m,CD=2DF=0.3 m.
∵ED=2.55 m,
∴EB=ED+BC-CD=2.55+1.5-0.3=3.75(m).
在Rt△AEB中,tan∠AEB=$\frac{AB}{EB}=\frac{0.75}{3.75}=\frac{1}{5}$,查表可得,∠AEB≈11.310°≈11°.
故为防止通道遮盖井盖,所铺设通道的坡角不得小于11度.
如图,

由题意,得DF=$\frac{1}{5}$AB=0.15 m,
∵斜坡AC的坡比为1∶2,
∴$\frac{AB}{BC}=\frac{1}{2}$,$\frac{DF}{CD}=\frac{1}{2}$,
∴BC=2AB=1.5 m,CD=2DF=0.3 m.
∵ED=2.55 m,
∴EB=ED+BC-CD=2.55+1.5-0.3=3.75(m).
在Rt△AEB中,tan∠AEB=$\frac{AB}{EB}=\frac{0.75}{3.75}=\frac{1}{5}$,查表可得,∠AEB≈11.310°≈11°.
故为防止通道遮盖井盖,所铺设通道的坡角不得小于11度.
22.(12分)已知△ABC是⊙O的内接三角形,AB = AC,点P是$\overset{\frown}{AB}$的中点,连接PA,PB,PC.
(1)如图(1),若∠BPC = 60°,求证:AC = $\sqrt{3}$AP;
(2)如图(2),若sin∠BPC = $\frac{24}{25}$,求tan∠PAB.
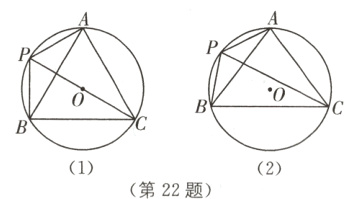
(1)如图(1),若∠BPC = 60°,求证:AC = $\sqrt{3}$AP;
(2)如图(2),若sin∠BPC = $\frac{24}{25}$,求tan∠PAB.

答案:
(1)
∵∠BPC=∠BAC=60°,AB=AC,
∴△ABC是等边三角形.
∵P是$\overset{\frown}{AB}$的中点,
∴$\overset{\frown}{AP}=\overset{\frown}{BP}$,
∴∠ACP=$\frac{1}{2}$∠ACB=30°.
∵∠APC=∠ABC=60°,
∴∠PAC=90°,
∴tan∠ACP=tan 30°=$\frac{AP}{AC}=\frac{\sqrt{3}}{3}$,
∴AC=$\sqrt{3}$AP.
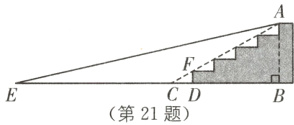
(2)如图,连接AO并延长交BC于点F,交PC与点E,过点E作EG⊥AC于点G,连接OC.

∵AB=AC,
∴AF⊥BC,BF=CF.
∵点P是$\overset{\frown}{AB}$的中点,
∴∠ACP=∠PCB,
∴EG=EF.
∵∠BPC=∠BAC=∠FOC,
∴sin∠FOC=sin∠BPC=$\frac{24}{25}$.
设CF=24a,则OC=OA=25a,
∴OF=7a,AF=32a,
∴在Rt△AFC中,AC=40a.
在Rt△AGE和Rt△AFC中,
∴sin∠FAC=$\frac{EG}{AE}=\frac{FC}{AC}$.
∴$\frac{EG}{32a - EG}=\frac{24a}{40a}$,
∴EG=12a,
∴EF=EG=12a,
∴tan∠PAB=tan∠PCB=$\frac{EF}{CF}=\frac{12a}{24a}=\frac{1}{2}$.
(1)
∵∠BPC=∠BAC=60°,AB=AC,
∴△ABC是等边三角形.
∵P是$\overset{\frown}{AB}$的中点,
∴$\overset{\frown}{AP}=\overset{\frown}{BP}$,
∴∠ACP=$\frac{1}{2}$∠ACB=30°.
∵∠APC=∠ABC=60°,
∴∠PAC=90°,
∴tan∠ACP=tan 30°=$\frac{AP}{AC}=\frac{\sqrt{3}}{3}$,
∴AC=$\sqrt{3}$AP.
(2)如图,连接AO并延长交BC于点F,交PC与点E,过点E作EG⊥AC于点G,连接OC.

∵AB=AC,
∴AF⊥BC,BF=CF.
∵点P是$\overset{\frown}{AB}$的中点,
∴∠ACP=∠PCB,
∴EG=EF.
∵∠BPC=∠BAC=∠FOC,
∴sin∠FOC=sin∠BPC=$\frac{24}{25}$.
设CF=24a,则OC=OA=25a,
∴OF=7a,AF=32a,
∴在Rt△AFC中,AC=40a.
在Rt△AGE和Rt△AFC中,
∴sin∠FAC=$\frac{EG}{AE}=\frac{FC}{AC}$.
∴$\frac{EG}{32a - EG}=\frac{24a}{40a}$,
∴EG=12a,
∴EF=EG=12a,
∴tan∠PAB=tan∠PCB=$\frac{EF}{CF}=\frac{12a}{24a}=\frac{1}{2}$.
23.(14分)(2022·扬州中考)如图(1),在△ABC中,∠BAC = 90°,∠C = 60°,点D在BC边上由点C向点B运动(不与点B,C重合),过点D作DE⊥AD,交射线AB于点E.


(1)分别探索以下两种特殊情形时线段AE与BE的数量关系,并说明理由.
①点E在线段AB的延长线上且BE = BD;
②点E在线段AB上且EB = ED.
(2)若AB = 6.
①当$\frac{DE}{AD}$ = $\frac{\sqrt{3}}{2}$时,求AE的长;
②直接写出运动过程中线段AE长度的最小值.


(1)分别探索以下两种特殊情形时线段AE与BE的数量关系,并说明理由.
①点E在线段AB的延长线上且BE = BD;
②点E在线段AB上且EB = ED.
(2)若AB = 6.
①当$\frac{DE}{AD}$ = $\frac{\sqrt{3}}{2}$时,求AE的长;
②直接写出运动过程中线段AE长度的最小值.
答案:
(1)①如图
(1),

在△ABC中,∠BAC=90°,∠C=60°,
∴∠ABC=30°.
∵BE=BD,
∴∠BDE=$\frac{1}{2}$∠ABC=15°,
∠BDA=90°-∠BDE=90°-15°=75°.
在△ABD中,∠BAD=180°-∠ABD-∠BDA=180°-30°-75°=75°,
∴∠BAD=∠BDA,
∴AB=BD=BE,
∴AE=2BE.
②如图
(2),

∵BE=DE,
∴∠EBD=∠EDB=30°,∠AED=60°,
∴在Rt△ADE中,∠EAD=30°,
∴AE=2ED,
∴AE=2BE.
(2)①如图
(3),分别过点A,E作BC的垂线,垂足为H,G,

易知△EGD∽△DHA(一线三垂直),
设DE=$\sqrt{3}$a,AD=2a,
则AE=$\sqrt{DE^{2}+AD^{2}}$=$\sqrt{7}$a,BE=6 - $\sqrt{7}$a.
在Rt△ABC中,∠ABC=30°,AB=6,
则AC=$\frac{AB}{\sqrt{3}}$=2$\sqrt{3}$,BC=2AC=4$\sqrt{3}$.
在Rt△BEG中,∠EBG=30°,BE=6 - $\sqrt{7}$a,则EG=$\frac{BE}{2}$=3 - $\frac{\sqrt{7}}{2}$a.
在Rt△AHC中,∠C=60°,AC=2$\sqrt{3}$,
则AH=$\frac{\sqrt{3}AC}{2}$=3,
DH=$\sqrt{AD^{2}-AH^{2}}$=$\sqrt{4a^{2}-9}$.
由△EGD∽△DHA,
得$\frac{ED}{AD}=\frac{EG}{DH}$,即$\frac{\sqrt{3}}{2}=\frac{3 - \frac{\sqrt{7}}{2}a}{\sqrt{4a^{2}-9}}$,
解得a1=$\frac{3}{5}\sqrt{7}$,a2=-3$\sqrt{7}$(舍去),
故AE=$\sqrt{7}$a=$\frac{21}{5}$.
②当∠EAD=30°,AE最小,最小为4.
(1)①如图
(1),

在△ABC中,∠BAC=90°,∠C=60°,
∴∠ABC=30°.
∵BE=BD,
∴∠BDE=$\frac{1}{2}$∠ABC=15°,
∠BDA=90°-∠BDE=90°-15°=75°.
在△ABD中,∠BAD=180°-∠ABD-∠BDA=180°-30°-75°=75°,
∴∠BAD=∠BDA,
∴AB=BD=BE,
∴AE=2BE.
②如图
(2),

∵BE=DE,
∴∠EBD=∠EDB=30°,∠AED=60°,
∴在Rt△ADE中,∠EAD=30°,
∴AE=2ED,
∴AE=2BE.
(2)①如图
(3),分别过点A,E作BC的垂线,垂足为H,G,

易知△EGD∽△DHA(一线三垂直),
设DE=$\sqrt{3}$a,AD=2a,
则AE=$\sqrt{DE^{2}+AD^{2}}$=$\sqrt{7}$a,BE=6 - $\sqrt{7}$a.
在Rt△ABC中,∠ABC=30°,AB=6,
则AC=$\frac{AB}{\sqrt{3}}$=2$\sqrt{3}$,BC=2AC=4$\sqrt{3}$.
在Rt△BEG中,∠EBG=30°,BE=6 - $\sqrt{7}$a,则EG=$\frac{BE}{2}$=3 - $\frac{\sqrt{7}}{2}$a.
在Rt△AHC中,∠C=60°,AC=2$\sqrt{3}$,
则AH=$\frac{\sqrt{3}AC}{2}$=3,
DH=$\sqrt{AD^{2}-AH^{2}}$=$\sqrt{4a^{2}-9}$.
由△EGD∽△DHA,
得$\frac{ED}{AD}=\frac{EG}{DH}$,即$\frac{\sqrt{3}}{2}=\frac{3 - \frac{\sqrt{7}}{2}a}{\sqrt{4a^{2}-9}}$,
解得a1=$\frac{3}{5}\sqrt{7}$,a2=-3$\sqrt{7}$(舍去),
故AE=$\sqrt{7}$a=$\frac{21}{5}$.
②当∠EAD=30°,AE最小,最小为4.
查看更多完整答案,请扫码查看


