《2025年单元双测全优测评卷九年级数学下册人教版》

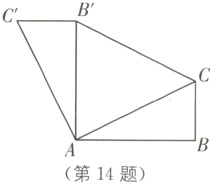
14. 如图，在Rt△ABC中，∠B=90°，AB=2，BC=1. 将△ABC绕点A逆时针方向旋转90°得到△AB′C′，连接B′C，则tan∠ACB′=________.

答案： $\frac{4}{3}$

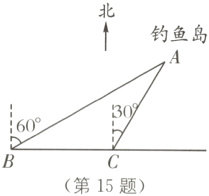
15. 如图，我国的一艘海监船在钓鱼岛A附近沿正东方向航行，船在点B时测得钓鱼岛A在船的北偏东60°方向，船以50海里/时的速度继续航行2小时后达到点C，此时钓鱼岛A在船的北偏东30°方向，请问船继续航行________海里与钓鱼岛A的距离最近.

答案： 50

16. 在△ABC中，∠ABC=60°，AD为BC边上的高，AD=6$\sqrt{3}$，CD=1，则BC的长为________.

答案：
7或5 [解析]在Rt△ABD中，∠ABC = 60°，AD = 6$\sqrt{3}$，
∴BD = $\frac{AD}{\tan B}$ = $\frac{6\sqrt{3}}{\sqrt{3}}$ = 6.
如图
(1)，BC = BD + CD = 6 + 1 = 7；
如图
(2)，BC = BD - CD = 6 - 1 = 5.

(第16题)

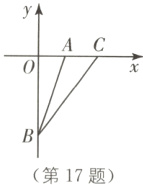
17.(2023·广元中考)如图，在平面直角坐标系中，已知点A(1，0)，点B(0，－3)，点C在x轴上，且点C在点A右方，连接AB，BC，若tan∠ABC=$\frac{1}{3}$，则点C的坐标为 ________.

答案：
($\frac{9}{4}$,0) [解析]如图，过点A作AD⊥BC，垂足为D.

∵A(1,0)，B(0,-3)，
∴OA = 1，OB = 3，
∴tan∠OBA = $\frac{1}{3}$.
∵tan∠ABC = $\frac{1}{3}$，
∴∠ABO = ∠ABC.
∵AO⊥BO，AD⊥BC，BA是∠OBC的平分线，
∴AO = AD = 1.
∵$\frac{S_{\triangle ABO}}{S_{\triangle ABC}}$ = $\frac{\frac{1}{2}OA×OB}{\frac{1}{2}AC×OB}$ = $\frac{\frac{1}{2}OB×OA}{\frac{1}{2}BC×AD}$，
∴$\frac{AC}{OA}$ = $\frac{CB}{OB}$.
设C(m,0)，则AC = m - 1，BC = $\sqrt{3^{2}+m^{2}}$，
∴$\frac{m - 1}{1}$ = $\frac{\sqrt{3^{2}+m^{2}}}{3}$，解得m = $\frac{9}{4}$或m = 0(舍去)
∴C($\frac{9}{4}$,0).
关键提醒：本题考查了正切的定义、角平分线的性质、勾股定理，熟练掌握角平分线的定义是解题的关键.

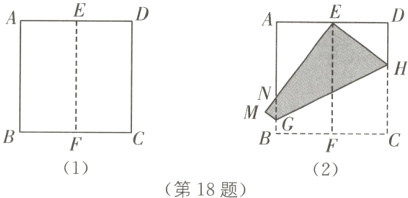
18. 如图(1)，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF. 如图(2)，展开后再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为点M，EM交AB于点N，则tan∠ANE=________.

答案： $\frac{3}{4}$

19.(6分)计算：
(1)(2023·济宁中考)计算：$\sqrt{12}-2\cos 30^{\circ}+|\sqrt{3}-2|+2^{-1}$；
(2)(2023·通辽中考)计算：$(\frac{1}{3})^{-2}+\tan 45^{\circ}-\sqrt{(-10)^{2}}$.

答案：
(1)原式 = 2$\sqrt{3}$ - 2×$\frac{\sqrt{3}}{2}$ + 2 - $\sqrt{3}$ + $\frac{1}{2}$
= 2$\sqrt{3}$ - $\sqrt{3}$ + 2 - $\sqrt{3}$ + $\frac{1}{2}$ = $\frac{5}{2}$.
(2)原式 = 9 + 1 - 10 = 0.