《2025年单元双测全优测评卷九年级数学下册人教版》

8. (2022·十堰中考)如图，坡角为α的斜坡上有一棵垂直于水平地面的大树AB，当太阳光线与水平线成45°角沿斜坡照下，在斜坡上的树影BC长为m，则大树AB的高为( ).

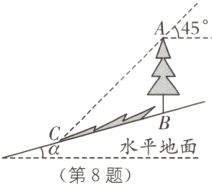
A. m(cos α - sin α)
B. m(sin α - cos α)
C. m(cos α - tan α)
D. $\frac{m}{\sin\alpha}-\frac{m}{\cos\alpha}$

答案： A

9. [跨学科综合](2023·深圳中考)爬坡时坡面与水平面夹角为α，则每爬1 m耗能(1.025 - cos α)J，若某人爬了1 000 m，该坡角为30°，则他耗能( ).(参考数据：$\sqrt{3}\approx1.732$，$\sqrt{2}\approx1.414$)

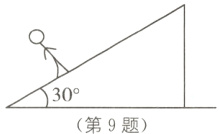
A. 58 J
B. 159 J
C. 1 025 J
D. 1 732 J

答案： B ［解析］由题意，得某人爬了 1 000 m，该坡角为$30^{\circ}$，则他耗能$=1000\times(1.025 - \cos30^{\circ})=1000\times(1.025 - \frac{\sqrt{3}}{2})\approx159$(J). 故选 B.

10. (2022·丽水中考)如图，已知菱形ABCD的边长为4，E是BC的中点，AF平分∠EAD交CD于点F，FG//AD交AE于点G，若cos B = $\frac{1}{4}$，则FG的长是( ).

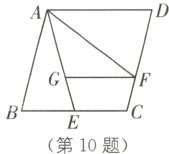
A. 3
B. $\frac{8}{3}$
C. $\frac{2\sqrt{15}}{3}$
D. $\frac{5}{2}$

答案：
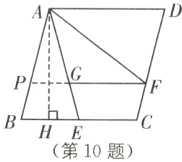
B ［解析］过点 A 作 AH 垂直 BC 于点 H，延长FG 交 AB 于点 P.
由题意可知，$AB = BC = 4$，E 是 BC 的中点，
$\therefore BE = 2$.
$\because\cos B=\frac{1}{4}$，$\therefore BH = 1$，即 H 是 BE 的中点，
$\therefore AB = AE = 4$.
又 AF 是$\angle DAE$的平分线，$AD// FG$，
$\therefore\angle FAG=\angle AFG$，即$AG = FG$.
又$PF// AD$，$AP// DF$，$\therefore PF = AD = 4$.
设$FG = x$，则$AG = x$，$EG = PG = 4 - x$，
$\because PF// BC$，$\therefore\angle AGP=\angle AEB=\angle B$.
$\therefore\cos\angle AGP=\frac{\frac{1}{2}PG}{AG}=\frac{2 - \frac{x}{2}}{x}=\frac{1}{4}$，解得$x=\frac{8}{3}$.

故选 B.

11. 已知α为锐角，tan(90° - α) = $\sqrt{3}$，则α的度数为________.

答案： $30^{\circ}$

12. (2022·扬州中考)在△ABC中，∠C = 90°，a，b，c分别为∠A，∠B，∠C的对边，若b² = ac，则sin A的值为________.

答案：
$\frac{-1+\sqrt{5}}{2}$ ［解析］如图所示，
在$Rt\triangle ABC$中，
由勾股定理，知$a^{2}+b^{2}=c^{2}$.
$\because ac = b^{2}$，$\therefore a^{2}+ac = c^{2}$.
$\because a＞0$，$b＞0$，$c＞0$，
$\therefore\frac{a^{2}+ac}{c^{2}}=\frac{c^{2}}{c^{2}}$，
即$(\frac{a}{c})^{2}+\frac{a}{c}=1$.
解得$\frac{a}{c}=\frac{-1+\sqrt{5}}{2}$或$\frac{a}{c}=\frac{-1-\sqrt{5}}{2}$(舍去).
$\therefore$在$Rt\triangle ABC$中，$\sin A=\frac{a}{c}=\frac{-1+\sqrt{5}}{2}$.

13. 在△ABC中，AD是BC边上的高，AD = 6，AC = 10，tan∠BAD = $\frac{1}{3}$，则△ABC的面积为________.

答案： 18 或 30

14. 如图，在Rt△ABC中，斜边BC上的高AD = 4，cos B = $\frac{4}{5}$，则AC =________.

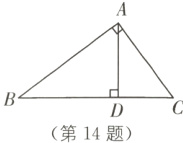
答案： 5