2025年学考A加同步课时练八年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学考A加同步课时练八年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
5.如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E,使AE//BC,连接AE.
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积=________;
②若AB=10,则BC=________时,四边形ADCE是正方形.
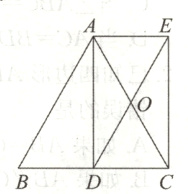
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积=________;
②若AB=10,则BC=________时,四边形ADCE是正方形.

答案:
(1)证明:$\because$点$O$是$AC$中点,
$\therefore AO = OC$,
$\because OE = OD$,
$\therefore$四边形$ADCE$是平行四边形,
$\because AD$是等腰$\triangle ABC$底边$BC$上的高,
$\therefore\angle ADC = 90^{\circ}$,
$\therefore$四边形$ADCE$是矩形.
(2)解:①$\because AD$是等腰$\triangle ABC$底边$BC$上的高,$BC = 16$,$AB = 17$,
$\therefore BD = CD = 8$,$AB = AC = 17$,$\angle ADC = 90^{\circ}$,
由勾股定理得:$AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{17^{2}-8^{2}} = 15$,
$\therefore$四边形$ADCE$的面积是$AD\times DC = 15\times8 = 120$.
②当$AB = 10$,$BC = 10\sqrt{2}$时,四边形$ADCE$是正方形,理由如下:
$\because AB = AC = 10$,$BC = 10\sqrt{2}$,
$\therefore AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{10^{2}-(5\sqrt{2})^{2}} = 5\sqrt{2}=DC$,
$\because AD\perp BC$,
$\therefore$四边形$ADCE$是正方形;
故答案为$120$;$10\sqrt{2}$.
(1)证明:$\because$点$O$是$AC$中点,
$\therefore AO = OC$,
$\because OE = OD$,
$\therefore$四边形$ADCE$是平行四边形,
$\because AD$是等腰$\triangle ABC$底边$BC$上的高,
$\therefore\angle ADC = 90^{\circ}$,
$\therefore$四边形$ADCE$是矩形.
(2)解:①$\because AD$是等腰$\triangle ABC$底边$BC$上的高,$BC = 16$,$AB = 17$,
$\therefore BD = CD = 8$,$AB = AC = 17$,$\angle ADC = 90^{\circ}$,
由勾股定理得:$AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{17^{2}-8^{2}} = 15$,
$\therefore$四边形$ADCE$的面积是$AD\times DC = 15\times8 = 120$.
②当$AB = 10$,$BC = 10\sqrt{2}$时,四边形$ADCE$是正方形,理由如下:
$\because AB = AC = 10$,$BC = 10\sqrt{2}$,
$\therefore AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{10^{2}-(5\sqrt{2})^{2}} = 5\sqrt{2}=DC$,
$\because AD\perp BC$,
$\therefore$四边形$ADCE$是正方形;
故答案为$120$;$10\sqrt{2}$.
6.如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)△EFD≌△GFB;
(2)试判断四边形EBGD的形状,并说明理由;
(3)当△ABC满足条件_______时,四边形EBGD是正方形.(不用说明理由)
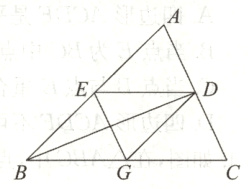
(1)△EFD≌△GFB;
(2)试判断四边形EBGD的形状,并说明理由;
(3)当△ABC满足条件_______时,四边形EBGD是正方形.(不用说明理由)

答案:
解:
(1)$\because EG$垂直平分$BD$,
$\therefore EB = ED$,$GB = GD$,
$\therefore\angle EBD=\angle EDB$.
$\because\angle EBD=\angle DBC$,
$\therefore\angle EDF=\angle GBF$.
在$\triangle EFD$和$\triangle GFB$中,
$\begin{cases}\angle EDF=\angle GBF,\\\angle EFD=\angle GFB,\\DF = BF,\end{cases}$
$\therefore\triangle EFD\cong\triangle GFB$.
(2)四边形$EBGD$是菱形.
理由:$\because EG$垂直平分$BD$,
$\therefore EB = ED$,$GB = GD$,
$\therefore\angle EBD=\angle EDB$,
$\because\angle EBD=\angle DBC$,
$\therefore\angle EDF=\angle GBF$,
在$\triangle EFD$和$\triangle GFB$中,
$\begin{cases}\angle EDF=\angle GBF,\\\angle EFD=\angle GFB,\\DF = BF,\end{cases}$
$\therefore\triangle EFD\cong\triangle GFB$,
$\therefore ED = BG$,
$\therefore BE = ED = DG = GB$,
$\therefore$四边形$EBGD$是菱形.
(3)当$\triangle ABC$是直角三角形,即$\angle ABC = 90^{\circ}$时,四边形$EBGD$是正方形,根据有一个角是直角的菱形是正方形可以得出.
故答案为$\angle ABC = 90^{\circ}$.
(1)$\because EG$垂直平分$BD$,
$\therefore EB = ED$,$GB = GD$,
$\therefore\angle EBD=\angle EDB$.
$\because\angle EBD=\angle DBC$,
$\therefore\angle EDF=\angle GBF$.
在$\triangle EFD$和$\triangle GFB$中,
$\begin{cases}\angle EDF=\angle GBF,\\\angle EFD=\angle GFB,\\DF = BF,\end{cases}$
$\therefore\triangle EFD\cong\triangle GFB$.
(2)四边形$EBGD$是菱形.
理由:$\because EG$垂直平分$BD$,
$\therefore EB = ED$,$GB = GD$,
$\therefore\angle EBD=\angle EDB$,
$\because\angle EBD=\angle DBC$,
$\therefore\angle EDF=\angle GBF$,
在$\triangle EFD$和$\triangle GFB$中,
$\begin{cases}\angle EDF=\angle GBF,\\\angle EFD=\angle GFB,\\DF = BF,\end{cases}$
$\therefore\triangle EFD\cong\triangle GFB$,
$\therefore ED = BG$,
$\therefore BE = ED = DG = GB$,
$\therefore$四边形$EBGD$是菱形.
(3)当$\triangle ABC$是直角三角形,即$\angle ABC = 90^{\circ}$时,四边形$EBGD$是正方形,根据有一个角是直角的菱形是正方形可以得出.
故答案为$\angle ABC = 90^{\circ}$.
查看更多完整答案,请扫码查看


