《2025年学考A加同步课时练八年级数学下册人教版》

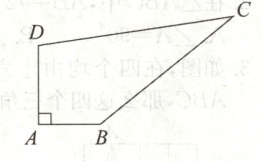
8. 为了绿化环境，我县某中学有一块四边形的空地ABCD，如图所示，学校计划在空地上种植草皮，经测量∠A = 90°，AB = 3 m，DA = 4 m，BC = 12 m，CD = 13 m.
（1）求出空地ABCD的面积；
（2）若每种植1平方米草皮需要200元，问总共需投入 多少元？

答案：
解：
(1)连接$BD$，
在$Rt\triangle ABD$中，
$BD^{2}=AB^{2}+AD^{2}=3^{2}+4^{2}=5^{2}$，
在$\triangle CBD$中，$CD^{2}=13^{2}$，$BC^{2}=12^{2}$，
而$12^{2}+5^{2}=13^{2}$，
即$BC^{2}+BD^{2}=CD^{2}$，
$\therefore\angle DBC = 90^{\circ}$，
则$S_{四边形ABCD}=S_{\triangle BAD}+S_{\triangle DBC}=\frac{1}{2}\cdot AD\cdot AB+\frac{1}{2}DB\cdot BC=\frac{1}{2}\times4\times3+\frac{1}{2}\times12\times5 = 36$.
(2)所以需费用$36×200 = 7200$(元).

9. 如图，△ABC中，AB = 10，BC = 6，AC = 8.
（1）求证：△ABC是直角三角形；
（2）若D是AC的中点，求BD的长.（结果保留根号）
　　　

答案： 证明：
(1)$\because AB^{2}=100$，$BC^{2}=36$，$AC^{2}=64$，
$\therefore AB^{2}=BC^{2}+AC^{2}$，
$\therefore\triangle ABC$是直角三角形.
(2)$CD = 4$，在$Rt\triangle BCD$中，$BD=\sqrt{BC^{2}+DC^{2}}=\sqrt{36 + 16}=\sqrt{52}=2\sqrt{13}$.